Bài 1:
Cho (O;R), và một điểm M nằm ngoài đường tròn (O) sao cho OM = 2R. Từ M vẽ tiếp
tuyến MA của đường tròn (O) (A là tiếp điểm)
a) Tính độ dài AM theo R
b) Từ A kẻ dây cung AB vuông góc với OM tại H. Chứng minh MB là tiếp tuyến của
đường tròn (O)
(vẽ hình)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
Câu 3:
a: Độ dài cung nhỏ AB là:
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=\dfrac{pi\cdot R\cdot2}{3}\)
Độ dài cung nhỏ BC là;
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=pi\cdot R\cdot\dfrac{2}{3}\)
b: \(S=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
c: Diện tích hình quạt tròn OAC là:
\(S_q=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot\dfrac{R^2}{3}\)
Diện tích tam giác OAC là:
\(S=\dfrac{1}{2}\cdot OA\cdot OC\cdot sin120=\dfrac{1}{4}\cdot R^2\)
Diện tích hình viên phân OAC là;
\(S_q-S=R^2\left(\dfrac{pi}{3}-\dfrac{1}{4}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
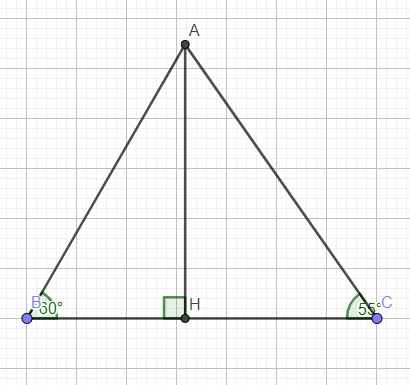
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)
