Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Ta có : \(1-\sqrt{3}\); \(\sqrt{2}-\sqrt{6}=\sqrt{2}\left(1-\sqrt{3}\right)\Rightarrow1-\sqrt{3}< \sqrt{2}\left(1-\sqrt{3}\right)\)
Vậy \(1-\sqrt{3}< \sqrt{2}-\sqrt{6}\)
b, Đặt A = \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}-\sqrt{2}\)(*)
\(\sqrt{2}A=\sqrt{8+2\sqrt{7}}-\sqrt{8-2\sqrt{7}}-2\)
\(=\sqrt{7}+1-\sqrt{7}+1-2=0\Rightarrow A=0\)
Vậy (*) = 0
1:
Ta có: \(\sqrt{2}-\sqrt{6}\)
\(=\sqrt{2}\left(1-\sqrt{3}\right)< 0\)
\(\Leftrightarrow1-\sqrt{3}< \sqrt{2}-\sqrt{6}\)

Ta có \(\left\{{}\begin{matrix}\left(2\sqrt{3}\right)^2=12\\\left(3\sqrt{2}\right)^2=18\end{matrix}\right.\) \(\Rightarrow2\sqrt{3}< 3\sqrt{2}\)
- Nếu \(m+1>0\Rightarrow m>-1\Rightarrow f\left(x\right)\) đồng biến \(\Rightarrow f\left(2\sqrt{3}\right)< f\left(3\sqrt{2}\right)\)
- Nếu \(m+1< 0\Rightarrow m< -1\Rightarrow f\left(x\right)\) nghịch biến \(\Rightarrow f\left(2\sqrt{3}\right)>f\left(3\sqrt{2}\right)\)
- Nếu \(m=-1\Rightarrow f\left(2\sqrt{3}\right)=f\left(3\sqrt{2}\right)=-2\)

a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.

a) Thay x=1 vào hàm số y=2x-1, ta được:
\(y=2\cdot1-1=2-1=2\)
Thay x=-1 vào hàm số y=2x-1, ta được:
\(y=2\cdot\left(-1\right)-1=-2-1=-3\)
Thay x=0 vào hàm số y=2x-1, ta được:
\(y=2\cdot0-1=-1\)
Thay x=2 vào hàm số y=2x-1, ta được:
\(y=2\cdot2-1=4-1=3\)
Vậy: F(1)=2; F(-1)=-3; F(0)=-1; F(2)=3
b)
x 1 -1 0 2 y=2x-1 2 -3 -1 3

Bài 1:
Thay x=1 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(1\right)=2\cdot1^2-5=2-5=-3\)
Thay x=-2 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(-2\right)=2\cdot\left(-2\right)^2-5=2\cdot4-5=3\)
Thay x=0 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(0\right)=2\cdot0^2-5=-5\)
Thay x=2 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(2\right)=2\cdot2^2-5=8-5=3\)
Thay \(x=\dfrac{1}{2}\) vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(\dfrac{1}{2}\right)=2\cdot\left(\dfrac{1}{2}\right)^2-5=2\cdot\dfrac{1}{4}-5=-\dfrac{9}{2}\)
Vậy: f(1)=-3; f(-2)=3; f(0)=-5; f(2)=3; \(f\left(\dfrac{1}{2}\right)=-\dfrac{9}{2}\)
Bài 1:
\(f(x)=2x^2-5\) thì:
$f(1)=2.1^2-5=-3$
$f(-2)=2(-2)^2-5=3$
$f(0)=2.0^2-5=-5$
$f(2)=2.2^2-5=3$
$f(\frac{1}{2})=2(\frac{1}{2})^2-5=\frac{-9}{2}$

Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 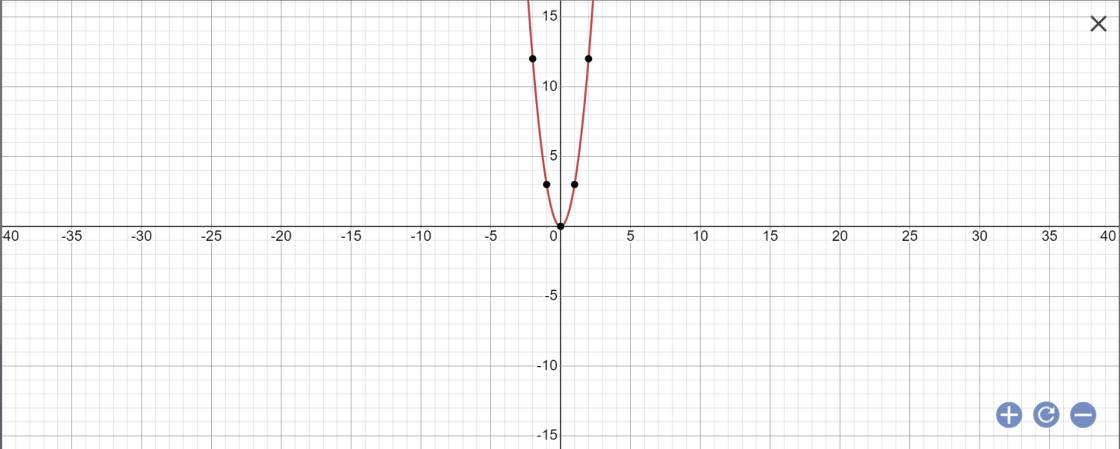

\(\sqrt{3}-\frac{5}{2}>\sqrt{3}-4\text{ vì }-\frac{5}{2}>-4\)
\(\Rightarrow2.\left(\sqrt{3}-\frac{5}{2}\right)>\sqrt{3}-4\)
\(\Rightarrow2.\sqrt{3}-5>\sqrt{3}-4\)

Ta có: 1<2
nên \(1-\sqrt{2}< 2-\sqrt{2}\)
\(\Leftrightarrow f\left(1-\sqrt{2}\right)>f\left(2-\sqrt{2}\right)\)(Vì hàm số y=f(x)=-x+4 nghịch biến trên R nên nếu \(x_1< x_2\) thì \(f\left(x_1\right)>f\left(x_2\right)\))
Ta có \(1-\sqrt{2}< 2-\sqrt{2}\) \(\Rightarrow-\left(1-\sqrt{2}\right)>-\left(2-\sqrt{2}\right)\) \(\Rightarrow-\left(1-\sqrt{2}\right)+4>-\left(2-\sqrt{2}\right)+4\) Mà \(f\left(1-\sqrt{2}\right)=-\left(1-\sqrt{2}\right)+4,f\left(2-\sqrt{2}\right)=-\left(2-\sqrt{2}\right)+4\)
\(\Rightarrow f\left(1-\sqrt{2}\right)>f\left(2-\sqrt{2}\right)\)