Cho cấp số nhân (Un) có u3=9 ;u6=243.Tính S10.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
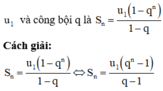

Chọn A
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên
là u 1 và công bội q là S n = u 1 ( 1 - q n ) 1 - q
Cách giải:
S n = u 1 ( 1 - q n ) 1 - q ⇔ S n = u 1 ( q n - 1 ) q - 1

Chọn B.
Gọi q là công bội của cấp số nhân (un)
Ta có 15u1 – 4u2 + u3 = 45 – 12q + 3q2 = 3(q – 2)2 + 33 ≥ 33 ∀ q
⇒ min(15u1 – 4u2 + u3) = 33 khi q = 2
Suy ra u13 = u1q12 = 3.212 = 12288.

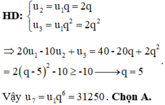

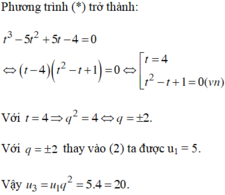
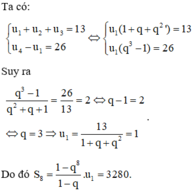
\(u_3=u_1\cdot q^2=9\left(1\right)\)
\(u_6=u_1\cdot q^5=243\left(2\right)\)
\(\dfrac{\left(1\right)}{\left(2\right)}=\dfrac{1}{q^3}=\dfrac{9}{243}=\dfrac{1}{27}\)
\(\Rightarrow q^3=27\)
\(\Rightarrow q=3\)
\(u_1=\dfrac{u_3}{q^2}=\dfrac{9}{3^2}=1\)\(\text{}\)
\(S_{10}=\dfrac{u_1\left(1-q^{10}\right)}{1-q}=\dfrac{1\left(3^{10}-1\right)}{3-1}=29524\)
tìm các số hạng của 1 cấp số nhân có 5 số hạng biết u1=3 và số hạng cuối là 243