cho tam giác ABC có AB<AC.M là trung điểm BC.Trên tia AM lấy D sao cho M là trung điểm AD.a)CM AB=CD,AB//CD,b)Vẽ AH vuông BC,DK vuông BC.cm AH=DK,c)Lấy N sao H là trung điểm AN,cm ND//BC,d)CM AK>HN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 11 2021
a: Xét tứ giác BNCH có
M là trung điểm của BC
M là trung điểm của HN
Do đó: BNCH là hình bình hành
16 tháng 8 2023
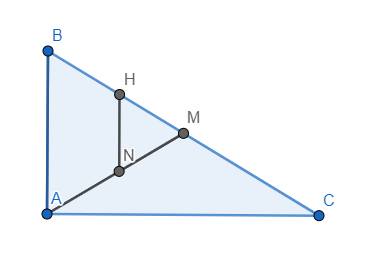
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)
4 tháng 8 2017
hình như đề sai hay sao ấy. đã cho tg ABC vuông cân tại A. đg cao AH r còn có đg trung tuyến AM
11 tháng 11 2021
a: Xét tứ giác AEHD có
\(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\)
Do đó: AEHD là hình chữ nhật
M
14 tháng 5 2022
tham khảo
a/ xét tứ giác AMCH , ta có
N là trung điểm AC [ gt]
N là trung điểm HM [ vì H đối xứng N qua M]
mà AC thuộc HM tại N
suy ra ; AMCH là hình bình hành [ dấu hiệu nhận biết ]
có AMCH là hình bình hành [ cma]
suy ra MC//AH [t/chat hình bình hành] M thuộc BC
suy ra AH//BM [1]
lại có M là trung điểm của BC [ gt ]
suy ra BM=MC
mà AH=BM [ tứ giác AMCH là hình bình hành] [2]
xét tứ giác ABMN , có ;
AH //BM [cmt]
AH= BM [cmt]
suy ra ABMH là hình bình hành [ dấu hiệu nhận biết ]
a) Xét ΔABM và ΔDCM có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔABM=ΔDCM(c-g-c)
Suy ra: AB=DC(hai cạnh tương ứng)
Ta có: ΔABM=ΔDCM(cmt)
nên \(\widehat{ABM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
b) Xét ΔAHM vuông tại H và ΔDKM vuông tại K có
MA=MD(gt)
\(\widehat{AMH}=\widehat{DMK}\)(hai góc đối đỉnh)
Do đó: ΔAHM=ΔDKM(cạnh huyền-góc nhọn)
Suy ra: AH=DK(hai cạnh tương ứng)
c)
Ta có: MA=MD(gt)
mà A,M,D thẳng hàng(gt)
nên M là trung điểm của AD
Xét ΔAND có
H là trung điểm của AN(gt)
M là trung điểm của AD(cmt)
Do đó: HM là đường trung bình của ΔAND(Định nghĩa đường trung bình của tam giác)
\(\Leftrightarrow\)HM//ND và \(HM=\dfrac{ND}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: HM//ND(cmt)
mà \(B\in HM\)(gt)
và \(C\in HM\)(gt)
nên ND//BC(đpcm)
d) Xét ΔAHK vuông tại H có AK là cạnh huyền(AK là cạnh đối diện với góc vuông AHK)
nên AK là cạnh lớn nhất trong ΔAHK(Định lí)
hay AK>AH
mà AH=HN(H là trung điểm của AN)
nên AK>HN(đpcm)