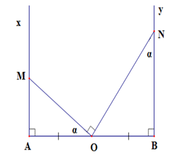
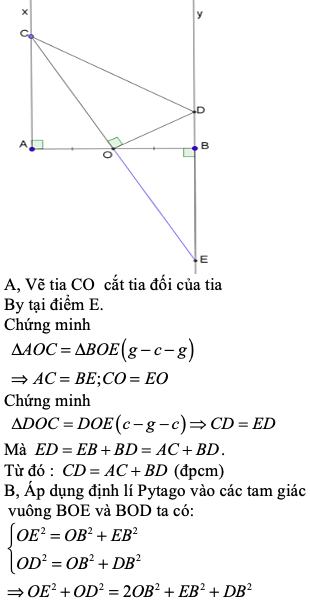
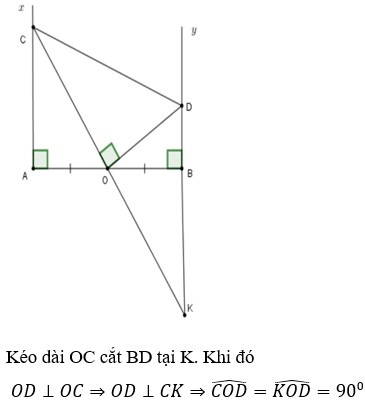
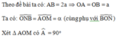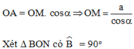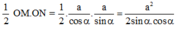Cho đoạn thẳng AB và O là trung điểm của nó. Vẽ về một phía của AB các tia Ax, By cùng vuông góc với AB. Các điểm M, N theo thứ tự dịch chuyển trên Ax, By sao cho các góc MON bằng 90 độ. Gọi I là trung điểm của MN. AB là tiếp tuyến của đường tròn (I;IO), MO là tia phân giác của góc AMN. Cm:
a) MN là tiếp tuyến của đường tròn đường kính AB
b) Khi các điểm M, N thay đổi trên Ax, By thì AM. BN không đổi
c) Tìm vị trí của M để MA + BN nhỏ nhất
d) Xđ vị trí của điểm H (H là chân đường vuông góc hạ từ O xuống MN) để diện tích tam giác AHB lớn nhất