cho hình chóp s.abcd có đáy abcd là hình vuông tâm o cạnh a, SA vuông góc với đáy; \(SA=a\sqrt{3}\) . tính cosin góc giữa 2 đg thg SB và AC?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6

a: (SAB) giao (ABCD)=AB
SA vuông góc AB, SA thuộc (SAB)
AD vuông góc AB, AD thuộc (ABCD)
=>((SAB);(ABCD))=góc SAD=90 độ

Đáp án A.
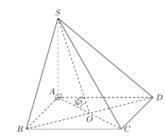
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
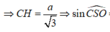
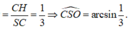

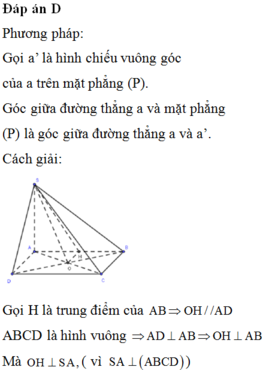
Đáp án D
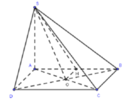
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 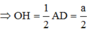
Tam giác SAH vuông tại A ![]()
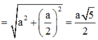
Tam giác SHO vuông tại H: 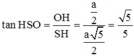


\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
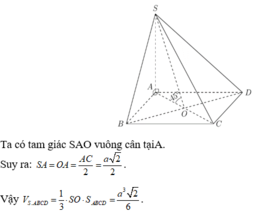



lại là chuyên mục toán hình :)) ( P/s hình t lấy từ gg xuống vì trên này khó vẽ... )
Ta có: \(\cos\left(\widehat{SB,AC}\right)=\left|\cos\left(\overrightarrow{SB},\overrightarrow{AC}\right)\right|=\dfrac{\left|\overrightarrow{SB}.\overrightarrow{AC}\right|}{SB.AC}\)
Mà: \(\overrightarrow{SB}.\overrightarrow{AC}=\left(\overrightarrow{SA}+\overrightarrow{AB}\right).\overrightarrow{AC}=\overrightarrow{SA}.\overrightarrow{AC}+\overrightarrow{AB}.\overrightarrow{AC}\)
\(=SA.AC.\cos\left(\overrightarrow{SA},\overrightarrow{AC}\right)+AB.AC.\cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)\)
thay số các kiểu ta đc \(\overrightarrow{SB}.\overrightarrow{AC}=a^2\) (1)
Hoàn toàn dễ dàng tính được \(SB=\sqrt{SA^2+AB^2}=2a\) ( tam giác SAB vuông tại A )
\(\Rightarrow SB.AC=2\sqrt{2}a^2\) (2)
Từ (1),(2) \(\Rightarrow\cos\left(\widehat{SB,AC}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Rightarrow\left(\widehat{SB,AC}\right)\simeq69^0\)
có 17' nữa t định ghi mà sợ ông kêu số xấu sai kết quả :)))
đúng r, nh mà tui bảo tính cosin thui ;))