Cho tam giác ABC có \(\widehat{C}=2\widehat{B}=4\widehat{A}\). CMR: \(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{BC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

X
9 tháng 2 2021
Gọi DD là điểm trên cạnh ACAC sao cho DB=DCDB=DCgọi EE là điểm trên cạnh BCBC sao cho CE=ABCE=AB7ˆC=180∘7C^=180∘ˆDBC=ˆDCB=12ˆABC=ˆABDDBC^=DCB^=12ABC^=ABD^⇒△ABD∼△ACB⇒△ABD∼△ACB (g, g)⇒ABAC=BDCB⇒ABAC=BDCB (1)△ABD=△ECD△ABD=△ECD (c, g, c) (2)(2)⇒ˆDEC=ˆDAB=4ˆC⇒DEC^=DAB^=4C^⇒ˆDEB=180∘−4ˆC=3ˆC⇒DEB^=180∘−4C^=3C^ (3)(2)⇒ˆEDC=ˆADB=2ˆC⇒EDC^=ADB^=2C^⇒ˆEDB=180∘−ˆEDC−ˆADB=3ˆC⇒EDB^=180∘−EDC^−ADB^=3C^ (4)từ (3, 4)⇒DB=EB⇒DB=EB (5)từ (1, 5)⇒ABAC=EBBC=1−ECBC=1−ABBC⇒ABAC=EBBC=1−ECBC=1−ABBC⇒ABAC+ABBC=1⇒ABAC+ABBC=1⇒1AB=1AC+1BC⇒1AB=1AC+1BC (đpcm)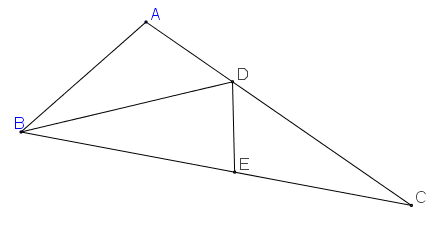 Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Hình gửi kèm
 Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/

19 tháng 10 2021
Bạn tk câu này mình làm rồi:
Cho ΔABC nhọn, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.CMR:a) DE=AH.SinAb) Cho AI là phân giác g... - Hoc24
nhớ đổi điểm I thành điểm D

29 tháng 6 2022
a: Vì \(\widehat{C}>30^0\) nên \(\sin C>\sin\left(30^0\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{AB}{BC}>\dfrac{1}{2}\)
hay AB>1/2BC
b: Vì \(\widehat{C}< 30^0\) nên \(\sin C< \sin30^0=\dfrac{1}{2}\)
=>AB<1/2BC