Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vận tốc vật ở góc lệch a: \(v_{\left(\alpha\right)}=\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}\) ( thuộc càng tốt )
lực căng dây:\(T_c=mg\left(3\cos\alpha_2-2\cos\alpha_1\right)\)
Bây giờ mình sẽ đi chứng minh 2 công thức trên :D
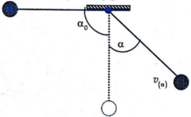
Chọn mốc tính thế năng tại vị trí thấp nhất của vật
Cơ năng của vật ứng với góc \(\alpha_1=45^0\) là:
\(W_1=W_{đ1}+W_{t1}=\dfrac{1}{2}mv_1^2+mgz_1=0+mgl\left(1-\cos\alpha_1\right)\)
Cơ năng của vật ứng với góc \(\alpha_2=30^0\) là:
\(W_2=W_{đ2}+W_{t2}=\dfrac{1}{2}mv_2^2+mgz_2=\dfrac{1}{2}mv_2^2+mgl\left(1-\cos\alpha_2\right)\)
Bỏ qua ma sát ( sức cản kk ) cơ năng được bảo toàn:
\(W_1=W_2\) \(\Leftrightarrow0+mgl\left(1-\cos\alpha_1\right)=\dfrac{1}{2}mv_2^2+mgl\left(1-\cos\alpha_2\right)\)
\(\Leftrightarrow v_2=\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}=\pm1,78\left(m/s\right)\)
Chọn trục tọa độ Oy hướng tâm:
Phương trình định luật II Niu tơn cho vật:
\(a=\dfrac{-P\cos\alpha+T_c}{m}\) trong đó: \(a=a_{ht}=\dfrac{v^2}{R}=\dfrac{v^2}{l}\) và v thì đã được chứng minh ở câu trên
Từ đấy ta có: \(\dfrac{\left(\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}\right)^2}{l}=\dfrac{-P\cos\alpha_2+T_c}{m}\)
\(\Rightarrow2mg\left(\cos\alpha_2-\cos\alpha_1\right)=-P\cos\alpha_2+T_c\)
\(\Rightarrow T_c=mg\left(3\cos\alpha_2-2\cos\alpha_1\right)=\) bạn thay số nốt hộ mình là xong :D hơi thấm mệt

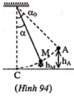
Chọn mặt phẳng ngang qua C làm gốc thế năng (hình 94)
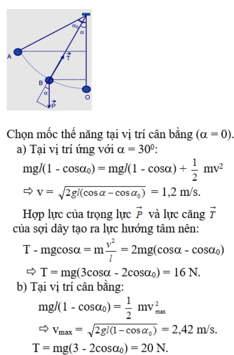
Cơ năng tại A ứng với góc lệch α = 45 0
![]()
Cơ năng tại M ứng với góc lệch α = 30 0
![]()
Định luật bảo toàn cơ năng: W A = W M
![]()
![]()

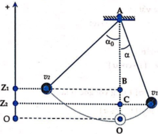
Đáp án D
+ Chọn mốc tính thế năng tại vị trí thấp nhất của vật
Cơ năng của vật ở vị trí 1 ứng với góc α 0 là
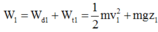
![]()
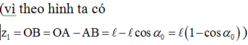
Cơ năng của vật ở vị trí 1 ứng với góc ![]() là
là
![]()
![]()
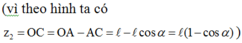
Bỏ qua sức cản không khí, thì cơ năng của vật là một đại lượng bảo toàn tức là
W1 = W2
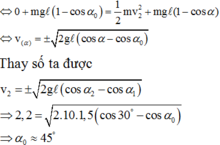

+ Chọn mốc tính thế năng tại vị trí thấp nhất của vật
Cơ năng của vật ở vị trí 1 ứng với góc α 1 = 45° là
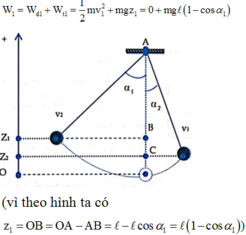
Co năng của vật ở vị trí 2 ứng với góc α 2 = 30° là
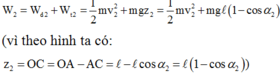
Bỏ qua sức cản không khí, thì cơ năng của vật là một đại lượng bảo toàn tức là W1=W2
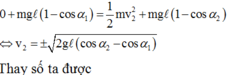
![]()
![]()