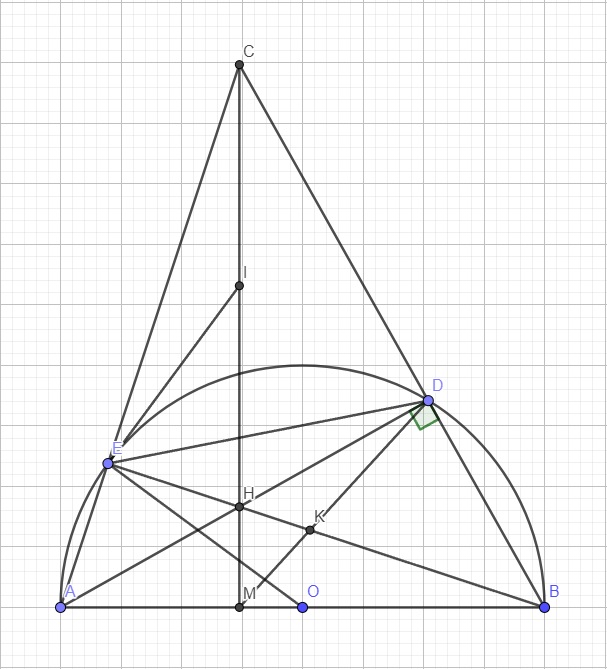
Cho nửa đường tròn tâm O và đường kính AB = 2R cố định . Lấy E và F là hai điểm thay đổi trên nửa đường tròn sao cho điểm E luôn thuộc cung AF . Gọi K là giao điểm của AE và BF , H là giao điểm của AF và BE .
a) Chứng minh EKFH nội tiếp
b) Tiếp tuyến tại F với nửa đường tròn cắt HK tại M . Chứng minh : M là trung điểm của HK
c) Chứng minh : khi E và F thay đổi trên nửa đườn tròn thì tổng ( AE.AK + BF.BK) không đổi

a) xét (o) có:
góc AEB=90 độ( góc nt chắn nửa đt)⇒góc BEK=90 độ
góc AFB=90 độ( góc nt chắn nửa đt)⇒góc AFK=90 độ
Xét tứ giác KEFH có:
góc BEK=90 độ
góc AFK=90 độ
⇒góc BEK +góc AFK=180 độ
⇒tứ giác KEFH nt ( tứ giác có tổng 2 góc đối= 180 độ)