một hộp đựng 18 viên bi trong đó có 8 bi trắng và 6 bi vàng, 4 bi xanh. Lấy ngẫu nhiên3 viên bi. Tính xác suất để:
a. 3 viên bi cùng màu
b. 3 viên bi khác màu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 5 2018
Ta có, số phần tử của không gian mẫu n ( Ω ) = C 10 2
Gọi các biến cố: D: “lấy được 2 viên đỏ” ; X: “lấy được 2 viên xanh” ;
V: “lấy được 2 viên vàng”
Ta có D, X, V là các biến cố đôi một xung khắc và C = D ∪ X ∪ V
P ( C ) = P ( D ) + P ( X ) + P ( V ) = C 4 2 C 10 2 + C 3 2 C 10 2 + C 2 2 C 10 2 = 2 9
Chọn đáp án B
CM
13 tháng 5 2019
Ta có: 
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có 
X: “lấy được 2 bi viên xanh” ta có: 
V: “lấy được 2 bi viên vàng” ta có: 
T: “ lấy được 2 bi màu trắng” ta có : 
Ta có D; X; V; T là các biến cố đôi một xung khắc và A= D ∪ X ∪ V ∪ T
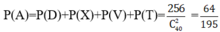
Chọn B.
CM
29 tháng 1 2019
Ta có: số phần tử của không gian mẫu là Ω = C 40 2
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có: n D = C 20 2 = 190 ;
X: “lấy được 2 bi viên xanh” ta có: n X = C 10 2 = 45 ;
V: “lấy được 2 bi viên vàng” ta có: n V = C 6 2 = 15 ;
T: “ lấy được 2 bi màu trắng” ta có: n T = C 4 2 = 6 .
Ta có D,X,V,T là các biến cố đôi một xung khắc và A = D ∪ X ∪ V ∪ T
Suy ra xác xuất để lấy được 2 viên bi cùng màu là:
P A = P D + P X + P V + P T = 256 C 40 2 = 64 195 .
Chọn đáp án D.
CM
9 tháng 9 2018
Chọn D
Cách 1:
Số phần tử của không gian mẫu: 
.
Gọi A là biến cố: “lấy ra 4 viên bi có đủ ba màu”
Ta xét các khả năng của biến cố A:
TH1: Lấy được 1 bi trắng, 1 bi xanh và 2 bi vàng, trường hợp này có 
(cách).
TH2: Lấy được 1 bi trắng, 2 bi xanh và 1 bi vàng, trường hợp này có 
(cách).
TH3: Lấy được 2 bi trắng, 1 bi xanh và 1 bi vàng, trường hợp này có 
(cách).
Số cách lấy 4 viên bi có đủ cả ba màu là: 
Xác suất cần tìm là 
Cách 2:
Số phần tử của không gian mẫu: 
Gọi A là biến cố: “lấy ra 4 viên bi không có đủ ba màu” .
Ta có: 
Xác suất của biến cố A là: 
Vậy xác suất cần tìm là: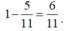 
.
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 12 2020
Không gian mẫu: \(C_{14}^5\)
Số cách để lấy 5 viên bi có đúng 1 màu: \(C_6^5+C_8^5\)
Số cách để lấy bi có đủ 2 màu: \(C_{14}^5-C_6^5-C_8^5\)
Xác suất: \(P=\dfrac{C_{14}^5-C_6^5-C_8^5}{C_{14}^5}\)
CM
9 tháng 4 2017
Chọn A
Lời giải
Không gian mẫu là số sách chọn ngẫu nhiên mỗi hộp 1 viên bi
Số phần tử của không gian mẫu là Ω = C 15 1 . C 18 1
Gọi X là biến cố "2 viên bi lấy ra từ mỗi hộp có cùng màu"
Ta có các kết quả thuận lợi cho biến cố X như sau
● Hộp A lấy ra 1 bi trắng và hộp B lấy ra 1 bi trắng, có C 4 1 . C 7 1 cách
● Hộp A lấy ra 1 bi đỏ và hộp B lấy ra 1 bi đỏ, có C 5 1 . C 6 1 cách
● Hộp A lấy ra 1 bi xanh và hộp B lấy ra 1 bi xanh, có C 6 1 . C 5 1 cách
Suy ra số phần tử của biến cố
Vậy xác suất cần tính
P ( X ) = Ω x Ω = 44 135
a) Không gian mẫu : \(\left|\Omega\right|=C^3_{18}=816\)
Biến cố A" 3 bi cùng màu"
Các trường hợp thuận lợi cho biến cố A "
TH1: 3 bi trắng \(C^3_8\)
TH2: 3 bi vàng \(C^3_6\)
TH3: 3 bi xanh \(C^3_4\)
=> \(\left|\Omega_A\right|=C^3_8+C^3_6+C^3_4=80\)
=> \(P\left(A\right)=\dfrac{80}{816}=\dfrac{5}{51}\)
b) Biến cố B" 3 bi khác màu"
Chọn mỗi màu 1 viên
Màu trắng 8 cách
Màu vàng 6 cách
Màu xanh 4 cách
=> \(\left|\Omega_B\right|=8\cdot6\cdot4=192\)
=> \(P\left(B\right)=\dfrac{\left|\Omega_B\right|}{\left|\Omega\right|}=\dfrac{192}{816}=\dfrac{4}{17}\)