Cho tam giác ABC có A=120 độ AB=14cm AC=16cm.Tính BC(lm theo cách lớp 7)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2017
ta có \(\widehat{A}\)=135 độ \(\Rightarrow\)\(\widehat{A}\)> \(\widehat{B}\)và \(\widehat{C}\)\(\Rightarrow\)cạnh BC là cạnh lớn nhất
ta có \(BC^2\)=\(AC^2\)+\(AB^2\)=\(\sqrt{5}\)+\(\sqrt{8}\)= 5+8 =13\(\Rightarrow\)BC =\(\sqrt{13}\)
21 tháng 1 2017
nhầm chỗ này nha ! sửa lại thành \(\left(\sqrt{5}\right)^2\)+\(\left(\sqrt{8}\right)^2\)mới đúng
FH
1
HV
5 tháng 11 2018
chu vi cua hinh tam giac a,b,c bang 1m65cm tong hai canh ab va ac bang 9cm, hoi canh bc dai bao nhieu cm la
VP
0
DT
0
26 tháng 5 2023
cosB=(16^2+BC^2-14^2)/(2*16*BC)
=>BC^2+60=32*BC*cos40
=>BC=21,76cm
S ABC=1/2*21,76*16*sin40=111,90cm2
VA
1
12 tháng 8 2021
bạn tự vẽ hình giúp mik nha
kẻ đường cao AH (H\(\in\)BC)
trong \(\Delta ABH\) vuoonng tại H có
BH=AB.cosB=14.cos40=10,7(cm)
AH=\(\sqrt{AB^2-BH^2}\)(pytago)=\(\sqrt{14^2-10,7^2}\)=9(cm)
trong \(\Delta AHC\) vuông tại H có
HC=\(\sqrt{AC^2-HA^2}\)(pytago)=\(\sqrt{11^2-9^2}\)=6,3(cm)
mà: BC=BH+HC=10,7+6,3=17(cm)
QT
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
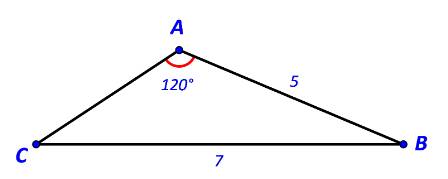
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.
TK
1
6 tháng 8 2021
Ta có: \(AC^2=CH\cdot BC\)
\(\Leftrightarrow CH^2+16HC-225=0\)
\(\Leftrightarrow CH^2+25HC-9HC-225=0\)
\(\Leftrightarrow CH=9\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12cm
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20cm
Ta có: BC=BH+HC
nên BC=9+16=25cm
tự vẽ hình nhé.
Kẻ AD⊥BC={D}AD⊥BC={D}
a, ΔABDΔABDcó: ˆADB=90oADB^=90o
⇒AD=AB.sinB⇔AD=16.sin30=8√3(cm)⇒AD=AB.sinB⇔AD=16.sin30=83(cm)
ΔABDΔABDcó: ˆADB=90oADB^=90o
⇒AB2=AD2+BD2⇒AB2=AD2+BD2(định lý Py-ta-go)
hay 162=(8√3)2+BD2162=(83)2+BD2
BD2=64BD2=64
BD=8(cm)BD=8(cm)
ΔADCΔADCcó: ˆADC=90oADC^=90o
⇒AC2=AD2+CD2⇒AC2=AD2+CD2(định lý Py-ta-go)
hay 142=(8√3)2+CD2142=(83)2+CD2
CD2=4CD2=4
CD=2(cm)CD=2(cm)
Ta có: BC=CD+BD=2+8=10(cm)
Kẻ BH \(\perp\)AC tại H
Ta có \(\widehat{BAH}=\widehat{A}-\widehat{BAC}=180^{\text{o}}-120^{\text{o}}=60^{\text{o}}\)
Lại có : tam giác AHB vuông tại H có \(\widehat{AHB}=\widehat{H}-\widehat{BAH}=90^{\text{o}}-60^{\text{o}}=30^{\text{o}}\)
=> \(AH=\frac{1}{2}AB=\frac{1}{2}.16=8\)(Vì trong tam giác vuông,cạnh đối diện với góc 30o bằng 1/2 cạnh huyền)
=>CH = AC + AH = 14 + 8 = 22 cm
Vì tam giác AHB vuông tại H => AH2 + HB2 = AB2
=> 82 + HB2 = 162
=> HB2 = 192
Lại có tam giác HBC vuông tại H
=> HC2 + HB2 = BC2
=> 222 + 192 = BC2
=> BC2 = 676
=> BC = 26 cm
Vậy BC = 26 cm