Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 8
SB=căn AB^2+SA^2=a*căn 7
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
=>SB vuông góc BC

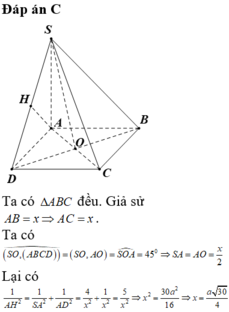
Gọi M là trung điểm AD \(\Rightarrow OM\perp AD\Rightarrow OM\perp\left(SAD\right)\)
\(\Rightarrow\widehat{MSO}\) là góc giữa SO và (SAD)
\(SM=\sqrt{SA^2+\left(\dfrac{AD}{2}\right)^2}=2\sqrt{2}\)
\(OM=\dfrac{1}{2}CD=1\)
\(tan\widehat{MSO}=\dfrac{OM}{SM}=\dfrac{1}{2\sqrt{2}}\) \(\Rightarrow\widehat{MSO}\approx19^028'\)

Đáp án A
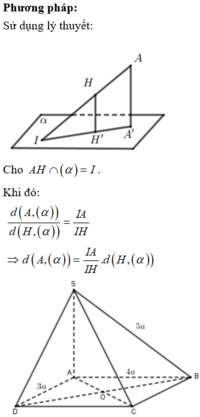
Phương pháp: Cách xác định góc giữa đường thẳng và mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
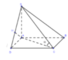
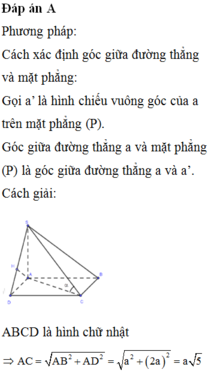
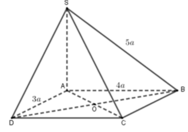
Cách giải: ABCD là hình chữ nhật ![]()
![]()
Vì SA ⊥ (ABCD) nên (SC;(ABCD)) = (SC;AC) = S C A ^
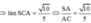
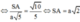
Ta có: AB//CD, CD ⊂ (SCD) => d(B;(SCD)) = d(A;(SCD))
Kẻ AH ⊥ SD, H ∈ SD
Ta có: 
![]()
Mà AH ⊥ SD => AH ⊥ (SCD) => d(A;(SCD)) = AH
Tam giác SAD vuông tại A,
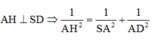
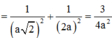
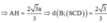

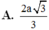
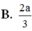
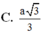
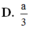

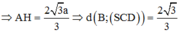

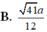
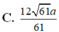
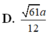
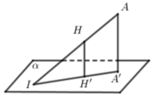
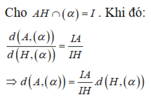

Do \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Kẻ \(AH\perp SD\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\sqrt{2}\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=\dfrac{\sqrt{2}}{2}\)
Trong đáp án không có đáp án này bạn ơi