bài 2 : 1 người đi từ A đến B dài 180km . Đi được 1/3 chặng đường thì người ấy giảm vận tốc đi 10km/h nên đến B chậm mất 1 giờ. Tính vận tốc lúc sau
giải bài toán bằng cách lập phương trình và giải thích tại sao lại lập phương trình đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường AB là x (km) (x > 0)
Thời gian người đó dự định đi là: x/36 (km)
Vận tốc đi thực tế là: 36 – 6 = 30 (km)
Thời gian thực tế người đó đi là: x/30 (km)
Do đến B chậm hơn dự tính 24’ = 2/5 h nên ta có phương trình:
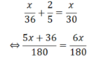
⇔ 5x + 36 = 6x
⇔ x = 36
Vậy quãng đường AB là 36 km.

Gọi độ dài quãng đường AB là x
Theo đề, ta có phương trình:
x/12-x/30=3
hay x=60

Giải
Theo đề bài ta có bảng sau:
| vận tốc(km/h) | thời gian(h) | quãng đường(km) | |
| Lúc đi | \(\frac{x}{6}\) | \(6\) | \(x\) |
| Lúc về | \(\frac{x}{5}+4\) | \(5\) | \(x\) |
Gọi chiều dài quãng đường AB là x\(\left(x\inℕ^∗\right)\)
Vận tốc lúc đi là:\(\frac{x}{6}\)(km/h)
Vận tốc lúc về là:\(\frac{x}{5}+4\)(km/h)
Ta có thời gian lúc về nhanh hơn thời gian lúc đi là:6-5=1(h)
Theo bảng trên ta có pt:\(\frac{x}{6}-\frac{x}{5}+4=1\)
Giải pt:\(\frac{x}{6}-\frac{x}{5}+4=1\)
\(\Leftrightarrow\frac{5x}{30}-\frac{6x}{30}+\frac{120}{30}=\frac{30}{30}\)
\(\Rightarrow5x-6x+120=30\)
\(\Leftrightarrow5x-6x=-120+30\)
\(\Leftrightarrow-x=-90\)
\(\Leftrightarrow x=90\left(tmđk\right)\)
Vậy chiều dài của quãng đường AB là 90km
#hoktot<3#

Gọi quãng đường AB là \(x\left(km\right)\left(x>0\right)\)
Thời gian người đó dự định đi là : \(\frac{x}{36}\left(km\right)\)
Thời gian người đó dự định đi là:
\(36-6=30\left(km\right)\)
Thời gian thực tế người đó đi là : \(\frac{x}{30}\left(km\right)\)
Do đến B chậm hơn dự tính \(24'=\frac{2}{5}h\) nên ta có phương trình :
\(\frac{x}{36}+\frac{2}{5}=\frac{x}{30}\)
\(\Leftrightarrow\frac{5x+36}{180}=\frac{6x}{180}\)
\(\Leftrightarrow5x+36=6x\)
\(\Leftrightarrow x=36\)
Vậy quãng đường AB là : \(36km\)
Chúc bạn học tốt !!!

Gọi quãng đường AB là x (km) (x > 0)
Thời gian người đó dự định đi là: x/36 (km)
Vận tốc đi thực tế là: 36 – 6 = 30 (km)
Thời gian thực tế người đó đi là: x/30 (km)
Do đến B chậm hơn dự tính 24’ = 2/5 h nên ta có phương trình:
⇔ 5x + 36 = 6x
⇔ x = 36
Vậy quãng đường AB là 36 km.
gọi quãng đường từ A đến B là x
thời gian dự định là t1
thời gian thực tế là t2
đổi 24 phút=2/5h
ta có
36t1=30t2
<=>36t1=30(t1+2/5)
<=>36t1=30t1+12
<=>6t1=12
<=>t1=2(h)
=> x=36.2=72
toán lớp 8 thật ak

Vận tốc lúc về :
\(50+10=60\left(\dfrac{km}{h}\right)\)
Quãng đường AB :
\(s=v.t=60.0,5=30\left(km\right)\)
Gọi độ dài quãng đường \(AB\) là \(x\left(x>0\right)\left(km\right)\)
Vận tốc lúc về của xe máy là: \(50+10=60\left(km/h\right)\)
Theo đề bài ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x}{60}=0,5\)
\(\Leftrightarrow x=150\) (TMĐK)
Vậy quãng đường \(AB\) dài \(150km\).

Bài 1:
Đổi \(45^,=\frac{3}{4}h\)
Gọi độ dài quãng đường AB là x(km) ĐK:\(x>0\)
Thời giạn mà người đó đi từ A đến B là \(\frac{x}{12}\left(h\right)\)
Thời gian mà người đó đi từ B về A là \(\frac{x}{10}\left(h\right)\)
Theo bài ra ta có pt: \(\frac{x}{10}-\frac{x}{12}=\frac{3}{4}\)
\(\Leftrightarrow\frac{x}{60}=\frac{3}{4}\)
\(\Leftrightarrow x=45\left(km\right)\)
Vậy quãng đường AB dài 45km
Bài 2:
Gọi độ dài quãng đường từ Bà Rịa đến thành phố Hồ Chí Minh là x(km) ĐK:x>0
Thời gian mà người thứ nhất đi hết quãng đường là \(\frac{x}{30}\left(h\right)\)
Thời gian mà người thứ hai đi hết quãng đường là \(\frac{x}{40}\left(h\right)\)
Ta có pt: \(\frac{x}{30}-\frac{x}{40}=1\)
\(\Leftrightarrow\frac{x}{120}=1\)
\(\Leftrightarrow x=120\left(km\right)\)
Vậy quãng đường từ Bà Rịa đến thành phố Hồ Chí Minh dài 120km
Bài 3:
Gọi vận tốc riêng của ca nô là x(km) ĐK:\(x>2\)
Vận tốc xuôi dòng là x+2(km/h)
Vận tốc ngược dòng là x-2(km/h)
Vì quãng đường không đổi nên ta có pt sau:
\(4\left(x+2\right)=5\left(x-2\right)\)
\(\Leftrightarrow4x+8=5x-10\)
\(\Leftrightarrow x=18\)
Do đó chiều dài khúc sông AB dài \(4.20=80\left(km\right)\)
Vậy chiều dài khúc sông AB dài 80km
Bài 4:
Gọi số người của đội II là x( x\(\in N,x>0\))
=> số người của đội I là 2x
Theo bài ra ta có pt sau:
\(x+10=\frac{4}{5}\left(2x-10\right)\)
\(\Leftrightarrow x=30\)
khi đó đội I có 60 người
Vậy đội I có 60 người
Đội II có 30 người
Gọi \(x\left(km/h\right)\) là vận tốc ban đầu \(\left(x>0\right)\)
Thời gian theo dự định là: \(\dfrac{180}{x}\left(h\right)\)
1/3 chặng đường dài là: \(\dfrac{1}{3}.180=60\left(km\right)\)
Thời gian đi trên 1/3 chặng đường đầu: \(\dfrac{60}{x}\left(h\right)\)
Quãng đường còn lại dài là: \(180-60=120\left(km\right)\)
Vận tốc trên quãng đường còn lại là: \(x-10\left(km/h\right)\)
Thời gian đi trên quãng đường này là: \(\dfrac{120}{x-10}\left(h\right)\)
Theo đề bài, ta có phương trình:
\(\dfrac{60}{x}+\dfrac{120}{x-10}-\dfrac{180}{x}=1\\ \Leftrightarrow\dfrac{60\left(x-10\right)}{x\left(x-10\right)}+\dfrac{120x}{x\left(x-10\right)}-\dfrac{180\left(x-10\right)}{x\left(x-10\right)}=\dfrac{x\left(x-10\right)}{x\left(x-10\right)}\\ \Rightarrow60\left(x-10\right)+120x-180\left(x-10\right)=x\left(x-10\right)\\ \Leftrightarrow60x-600+120x-180x+1800-x^2+10x=0\\ \Leftrightarrow-x^2+10x+1200=0\\ \Leftrightarrow-x^2+40x-30x+1200=0\Leftrightarrow-x\left(x-40\right)-30\left(x-40\right)=0\\ \Leftrightarrow\left(x-40\right)\left(-x-30\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-40=0\\-x-30=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=40\left(nhận\right)\\x=-30\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc lúc sau là \(40-10=30km/h\)
Gọi x(km/h)x(km/h) là vận tốc ban đầu (x>0)(x>0)
Thời gian theo dự định là: 180x(h)180x(h)
1/3 chặng đường dài là: 13.180=60(km)13.180=60(km)
Thời gian đi trên 1/3 chặng đường đầu: 60x(h)60x(h)
Quãng đường còn lại dài là: 180−60=120(km)180−60=120(km)
Vận tốc trên quãng đường còn lại là: x−10(km/h)x−10(km/h)
Thời gian đi trên quãng đường này là: 120x−10(h)120x−10(h)
Theo đề bài, ta có phương trình:
60x+120x−10−180x=1⇔60(x−10)x(x−10)+120xx(x−10)−180(x−10)x(x−10)=x(x−10)x(x−10)⇒60(x−10)+120x−180(x−10)=x(x−10)