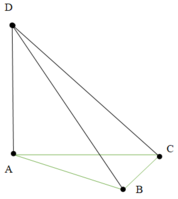
Cho tứ diện ABCD có \(DA\perp\left(ABC\right);AI\perp CD;AJ\perp BD\) a, Chứng minh AI⊥(BCD);BD⊥(AIJ)b, Chứng minh BCIJ nội tiếp đường tròn O' . Gọi O là trung điểm AB . Chứng minh OO'⊥(BCD)c, Tìm điểm cách đều 5 điểm A,B,C,I,Jd, Gọi K là giao điểm của IJ và (ABC). Chứng minh AK tiếp xúc với đường tròn ngoại tiếp tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Dễ thấy ∆ABC vuông tại A => SABC = 6
=> VS.ABC = 1 3 .6.5 = 10

Đáp án C
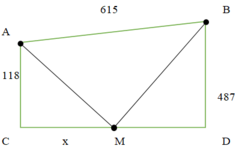
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD = 615 2 - ( 487 - 118 ) 2 = 492
Từ đề bài ta có: f(x) = x 2 + 118 2 + ( 492 - x ) 2 + 487 2
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = - 2 x 2 x 2 + 118 2 + 2 ( 492 - x ) 2 ( 492 - x ) 2 + 487 2
⇒ f’(x) = 0
⇔ ( 492 - x ) x 2 + 118 2 - x ( 492 - x ) 2 + 487 2 = 0
⇔ ( 492 - x ) 2 ( x 2 + 118 2 ) - x 2 ( ( 492 - x ) 2 + 487 2 ) = 0
⇔ x = 58056 605
Ta có bảng biến thiên
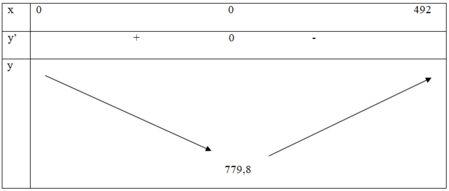
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
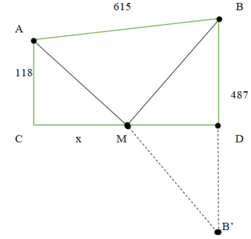
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇒ AM + MB ngắn nhất
⇒ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
=>AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng

Đáp án C
V A B C D = 1 3 . 3 4 .1 = 3 12
V D M N P V D A B C = D M D A . D N D B . D P D C = 1 8 ⇒ V D M N P = 3 96

Ta có
V D M N P V D A B C = D M D A . D N D B . D P D C = 1 2 . 1 2 . 3 4 = 1 8
Do đó 1 8 . 3 12 = 3 96
Đáp án C