Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD
a. Tứ giác ABDC là hình gì? Ví sao?
b. Tam giác ABC cần thêm điều kiện gì thì tứ giác ABCD là hnhf thoi
c. Qua A vẽ đường thẳng d song song với BC. Chứng minh rằng Ba điểm D, C, I thẳng hàng



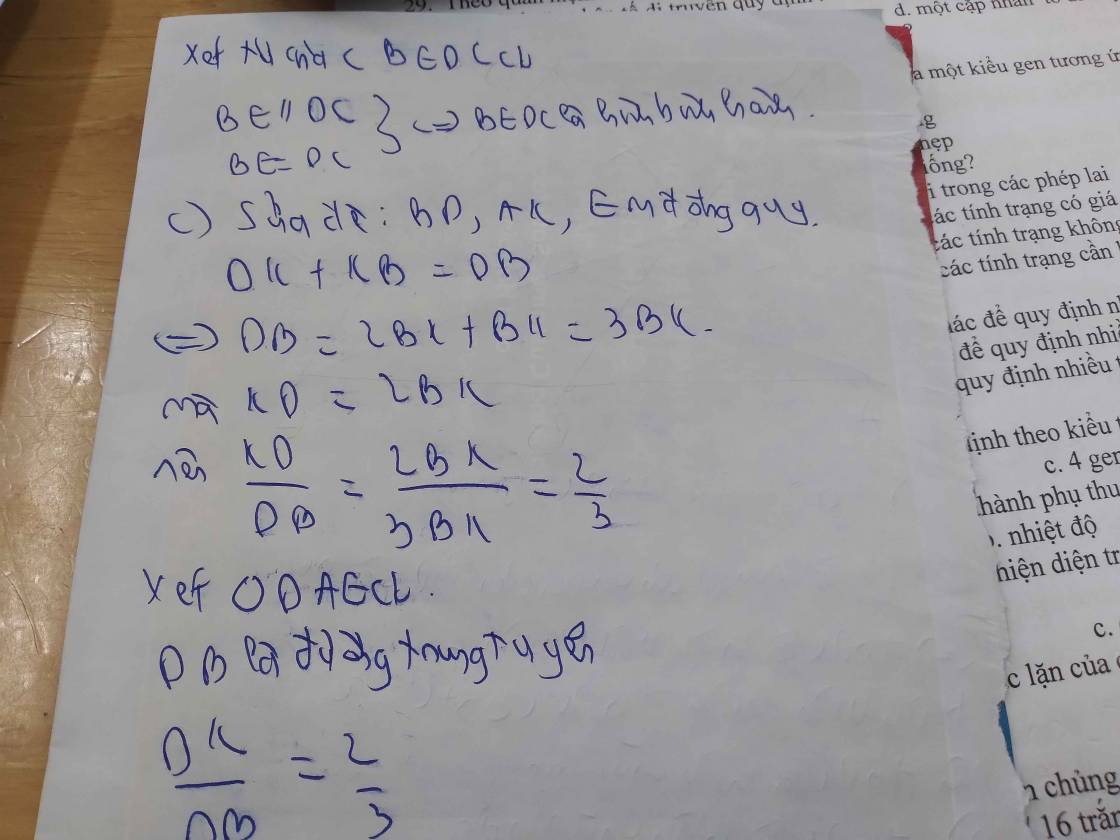

a, Xét tứ giác ABDC có: AM=MD (gt) ; BM=MC (gt)
=> ABDC là hình bình hành
b,Để ABDC là hình thoi => AB = AC => \(\Delta ABC\)cân
c, I đâu ra vậy bạn?