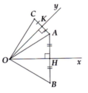
Cho góc ^xoy. Lấy A,C thuộc tia Ox sao cho OC<OA. Trên tia Oy lấy B và D sao cho OB=OA,OD=OC.
a) Chứng minh AD = BC và ∆ABC=∆BAD
b) Gọi I là giao điểm của AD và BC. Cho biết IA = IB. Chứng minh OI là tia phân giác của góc ^xoy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2022
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
27 tháng 11 2021
a
xét tam giác AOD và BCD có:
góc D chung,OB=OA,OC=OD
=>tam giác AOD=BCD=>BC=AD
vì OC+CA=OA,OD+DB=OB mà OC=OD,OA=OB
=>AC=BD
xét tam giác ADB và BCA có:
AC=BD,AB chung,BC=AD
=>ADB=BCA
b
xét tam giác OIA và OIB có
OA=OB,OI chung,IA=IB
=>tam giác OIA=OIB=>góc AOI=góc BOI=>OI là phân giác góc xOy
CM
10 tháng 11 2017
ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒ 
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.
CM
1 tháng 12 2018
Ox là đường trung trực của AB, O AB
Nên OA = OB
Tương tự ta có OA = OC
Từ đó suy ra ĐPCM
R
27 tháng 1 2022
a)
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
27 tháng 1 2022
c) Ta có:
ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: BOE=DOE
hay OE là tia phân giác của góc xOy
21 tháng 9 2023
Tham khảo:
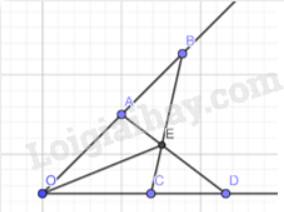
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{A}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)
16 tháng 5 2023
a: góc xOM=120 độ
b: AB=3+6=9cm
c: BC=AC=9/2=4,5cm
OC=4,5-3=1,5cm
16 tháng 5 2023
A. Ta có: Góc xOy = 90 độ (do hai trục Ox và Oy vuông góc với nhau)
Góc xOm = 120 độ => góc mOy + góc xOy + góc xOm = 360 độ (tổng góc bên trong của một tam giác)
=> Góc mOy = 150 độ
Do tia Om không trùng với tia Ox và tia Oy
=> Góc xOm = 120 độ
B.Ta có : OA+OA=AB
=> 6+3=AB
=> AB=6cm
C.vì C là trung điểm của AB nên ta có AC = CB = AB/2 = 4,5cm.
Vậy AC=4,5cm
Ta có : 0C=4,5-3=1,5cm
lỗi r nha
Loading