Cho các điểm A,B cố định thỏa mãn AB = a. Tìm tập hợp M thỏa mãn \(\overrightarrow{AM}.\overrightarrow{AB}=2a^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Lấy điểm A' đối xứng với A qua Ox \(\Rightarrow A\left(-2;-1\right)\)
M có tọa độ \(M\left(x;0\right)\)
Ta có \(AM+MB=A'M+MB\ge AB=\sqrt{4^2+5^2}=\sqrt{41}\)
\(min=41\Leftrightarrow M,A',B\) thẳng hàng
\(\Leftrightarrow\overrightarrow{A'M}=k\overrightarrow{A'B}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2=k.4\\1=k.5\end{matrix}\right.\Rightarrow x=-\dfrac{6}{5}\Rightarrow M\left(-\dfrac{6}{5};0\right)\)
2.
Gọi N là trung điểm BC
\(\overrightarrow{MA}.\left(\overrightarrow{MB}+\overrightarrow{MC}\right)=0\)
\(\Leftrightarrow2\overrightarrow{MA}.\overrightarrow{MN}=0\)
\(\Leftrightarrow2MA.MN.cosAMN=0\)
\(\Leftrightarrow\left[{}\begin{matrix}MA=0\\MN=0\\cosAMN=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}M\equiv A\\M\equiv N\\\widehat{AMN}=90^o\end{matrix}\right.\)
\(\Rightarrow M\) thuộc đường tròn đường kính AN

Gt ⇒ \(2\left|\overrightarrow{MC}+\overrightarrow{MA}+\overrightarrow{MB}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Do G là trọng tâm của ΔABC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\)
⇒ VT = 6MG
I là trung điểm của BC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\)
⇒ VP = 6MI
Khi VT = VP thì MG = MI
Vậy tập hợp các điểm M thỏa mãn ycbt là đường trung trực của đoạn thẳng IG

a) Ta có: \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng hướng và \(AC = \frac{1}{2}AB\).
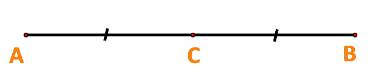
Vậy C là trung điểm của AB.
b) Ta có: \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} = - \overrightarrow {AC} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AD} ,\overrightarrow {AC} \) ngược hướng và \(AD = AC\).
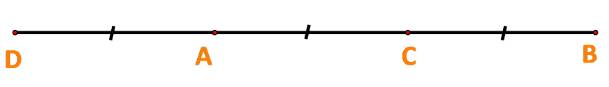
Vậy A là trung điểm DC.

Lời giải:
Gọi $I$ là trung điểm của $AB$ thì \(\overrightarrow{IA}; \overrightarrow{IB}\) là hai vector đối nhau.
Ta có:
\(\overrightarrow{MA}.\overrightarrow{MB}=-16\)
\(\Leftrightarrow (\overrightarrow{MI}+\overrightarrow{IA})(\overrightarrow{MI}+\overrightarrow{IB})=-16\)
\(\Leftrightarrow MI^2+\overrightarrow{MI}(\overrightarrow{IA}+\overrightarrow{IB})+\overrightarrow{IA}.\overrightarrow{IB}=16\)
\(\Leftrightarrow MI^2+\overrightarrow{IA}(-\overrightarrow{IA})=-16\)
\(\Leftrightarrow MI^2-IA^2=-16\)
\(\Leftrightarrow MI^2=-16+IA^2=-16+(\frac{AB}{2})^2=-16+4^2=0\)
Do đó \(M\equiv I\) hay $M$ là trung điểm của $AB$. Tập hợp điểm $M$ là \(\left\{I\right\}\)
chị có thể giải thích đoạn MI^2+vectoIA(trừ vectoIA)=-16 không ạ?
Tham khảo:
Cho 2 điểm cố định A B và AB = a. Tìm tập hợp điểm M thỏa mãn AM . AB = 2a^2