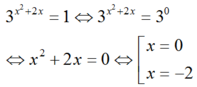Tìm nghiệm nguyên của phương trình:x6+3x2+1=y4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
0
TQ
0
30 tháng 1 2023
=>3x^2-c=ax^2-2ax+a-bx+b
=>3x^2-c-a*x^2+2ax-a+bx-b=0
=>x^2(3-a)+x(2a+b)-a-b-c=0
Để phương trình luôn có nghiệm thì 3-a=0 và 2a+b=0 và a+b+c=0
=>a=3; b=-6; c=-a-b=-3+6=3
VD
13 tháng 3 2022
Ta có: \(\Delta=5^2-5.3.1=25-12=13>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-1\end{matrix}\right.\)
\(K=\left(3x_1-1\right)\left(3x_2-1\right)+3\\ =3x_1x_2-3x_2-3x_1+1+3=3.\left(-1\right)-3\left(x_1+x_2\right)+4\\ =-3+4-3\left(-5\right)\\ =1+15\\ =16\)
CM
30 tháng 1 2019
Đáp án B
PT ⇔ x 2 + 4 x − 1 = 3 ⇔ x 2 + 4 x − 4 = 0 ⇔ x = − 2 + 2 2 x = − 2 − 2 2 ⇒ S = − 2 − 2 2 ; − 2 + 2 2
