Hình chiếu bằng của khối chóp cụt đều là hình gì ? Add ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 3 2019
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
CM
28 tháng 12 2018
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
CM
25 tháng 6 2019
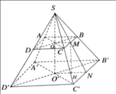
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
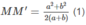
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :
10 tháng 5 2017
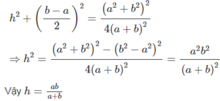
Xét hình chóp cụt đều ABCD.AB'C'D'
Gọi M ,M' thứ tự là trung điểm của BC , B'C' . Khi đó MM' là đường cao của hình thang cân BCC'B' . Do đó diện tích xung quanh của hình chóp cụt đều là :
\(S_{xq}=4.\dfrac{a+b}{2}.MM'=\left(2a+2b\right).MM'\)
Từ giả thiết , ta có :
\(\left(2a+2b\right).MM'=a^2+b^2hayMM'=\dfrac{a^2+b^2}{2\left(a+b\right)}\left(1\right)\)
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O') . Trong mặt phẳng (OMM'O') , kẻ MH \(\perp\) O'M' . Khi đó : \(HM'=O'M'-O'H=\dfrac{b-a}{2}\)
Trong tam giác vuông MHM' ta có :
\(MM'^2=MH^2+HM'^2=h^2+\left(\dfrac{b-a}{2}\right)^2\left(2\right)\)
Từ (1) và (2) suy ra :
\(h^2+\left(\dfrac{b-a}{2}\right)^2=\dfrac{\left(a^2+b^2\right)^2}{4\left(a+b\right)^2}\)
\(\Rightarrow h^2=\dfrac{\left(a^2+b^2\right)^2-\left(b^2-a^2\right)^2}{4\left(a+b\right)^2}=\dfrac{a^2b^2}{\left(a+b\right)^2}\)
Vậy \(h=\dfrac{ab}{a+b}\)
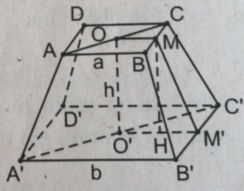
Hình chiếu bằng của khối chóp cụt đều là hai hình vuông bằng hai hình vuông của hai đáy với 4 đoạn thẳng nối các đỉnh tương ứng của 2 hình vuông