Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)

Sửa b)`->` x nguyên để f(x) nguyên
a)TXĐ:`{(x>=0),(sqrtx-1 ne 0):}`
`<=>{(x>=0),(sqrtx ne 1):}`
`=>x>=0,x ne 1`
`b)f(x) in ZZ=>sqrtx+1 vdots sqrtx-1`
`=>sqrtx-1+2 vdots sqrtx-1`
`=>2 vdots sqrtx-1`
`=>sqrtx-1 in Ư(2)`
`=>sqrtx-1 in {+-1;2}`
`=>sqrtx in {0;2;3}`
`=>x in {0;4;9}`
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Để f(x) nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)
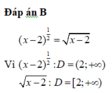
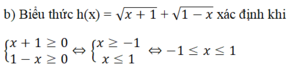

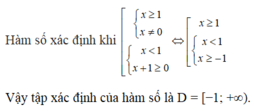
\(\sqrt{x+1}+\dfrac{1}{x}\)
\(đk:\left\{{}\begin{matrix}x+1\ge0\\x\ne0\end{matrix}\right.< =>\left\{{}\begin{matrix}x\ge-1\\x\ne0\end{matrix}\right.\)