cot 40° + cot 30° bằng bao nhiêu ?
cho e cách lm vs ạ
e cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 1 2020
Chọn C.
Nhân cả tử và mẫu với tanα và chú ý tanα.cotα = 1 ta được:
1
1
TM
23 tháng 7 2023
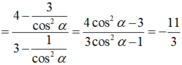
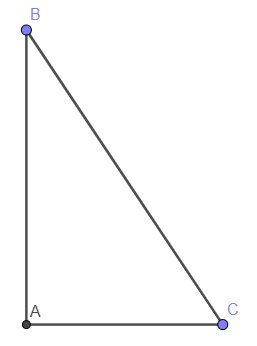
Xét \(\Delta ABC\) vuông tại A có:
\(sin\left(B\right)=\dfrac{AC}{BC}\)
\(cotg\left(C\right)=\dfrac{AC}{AB}\)
BC là cạnh huyền của \(\Delta ABC\) \(\left(AB,AC< BC\right)\)
\(\Rightarrow\dfrac{AC}{BC}< \dfrac{AC}{AB}\Rightarrow sin\left(B\right)< cotg\left(C\right)\)
30 tháng 10 2019
gọi H là trực tâm các đường cao BI,CF,AE
Ta có : \(\cot A=\frac{AI}{BI}=\frac{AF}{FC}\) ; \(\cot B=\frac{BE}{AE}=\frac{BF}{FC}\); \(\cot C=\frac{CI}{BI}=\frac{CE}{AE}\)
\(\Rightarrow\cot A.\cot B+\cot B.\cot C+\cot C.\cot A=\frac{AI}{BI}.\frac{BE}{AE}+\frac{BF}{FC}.\frac{CI}{BI}+\frac{CE}{AE}.\frac{AF}{FC}\)
\(\Delta AFH~\Delta AEB\left(g.g\right)\Rightarrow\frac{AF}{AH}=\frac{AE}{AB}\Rightarrow\frac{AF}{AE}=\frac{AH}{AB}\)
\(\Rightarrow\frac{CE}{AE}.\frac{AF}{FC}=\frac{CE.AH}{AB.CF}=\frac{S_{ACH}}{S_{ABC}}\)
Tương tự : \(\frac{AI}{BI}.\frac{BE}{AE}=\frac{S_{BHA}}{S_{ABC}};\frac{BF}{FC}.\frac{CI}{BI}=\frac{S_{BCH}}{S_{ABC}}\)
\(\Rightarrow\cot A.\cot B+\cot B.\cot C+\cot C.\cot A=\frac{S_{BHA}+S_{BHC}+S_{AHC}}{S_{ABC}}=1\)
DN
0
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 8 2021
\(G=cot^2x-sin^2x.cot^2x+1-cot^2x=1-sin^2x.cot^2x\)
\(=1-sin^2x.\dfrac{cos^2x}{sin^2x}=1-cos^2x=sin^2x\)
2.
\(tana+cota=2\Rightarrow\left(tana+cota\right)^2=4\)
\(\Rightarrow tan^2a+cot^2a+2tana.cota=4\)
\(\Rightarrow tan^2a+cot^2a+2=4\)
\(\Rightarrow tan^2a+cot^2a=2\)