Cho tam giác ABC cân tại A, đường cao AD, phân giác BE. Tính các góc của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TK
0

PS
0


CM
2 tháng 12 2019
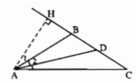
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)
Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º
+) Xét tam giác AHB vuông tại H ta có:
∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)
Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º
+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)
Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên
∠(BAC) = (180º − 112º) : 2 = 34o
+) Do AD là tia phân giác của góc BAC nên
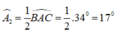
+ Từ đó
∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.
Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º
Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º
Đặt DH = x. Trên tia đối của tia DA em lấy điểm E sao cho DE = DH = x
=> tam giác BEH cân tại B => ^DBE = ^DBH (1) và BE = BH = 30
Mặt khác : ^ABD = ^ACD = ^BHD (2) ( góc có cạnh tương ứng vuông góc AC _|_ BH; CD _|_ DH)
(1) + (2) : ^ABD + ^DBE = ^BHD + ^DBH = 90o => tam giác ABE vuông tại B
Trong tg ABE vuông tại B đường cao BD nên ta có hệ thức:
DE.AE = BE²
<=> DE(AH + DH + DE) = BE²
<=> x(2x + 14) = 900
<=> 2x² + 14x - 900 = 0
Giải ra x = 18 ( loại nghiệm x = - 25)
=> AD = AH + DH = 14 + 18 = 32