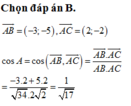trong mặt phẳng oxy ,cho tam giác ABC biết A(2;-1) và I(1;0) là trung điểm BC .Tìm tọa độ trọng tâm tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)
\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)
\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)
Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)

\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)
\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)
\(BC=\left(-3;4\right)\Rightarrow BC=5\)
Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)

\(AB=\sqrt{\left(0+1\right)^2+\left(2+3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left(2+1\right)^2+\left(1+3\right)^2}=\sqrt{3^2+4^2}=5\)
\(BC=\sqrt{\left(2-0\right)^2+\left(1-2\right)^2}=\sqrt{5}\)
=>\(C=\sqrt{26}+5+\sqrt{5}\left(cm\right)\)

\(AB=\sqrt{\left(5-1\right)^2+\left(-3+1\right)^2}=2\sqrt{5}\)
\(AC=\sqrt{\left(0-1\right)^2+\left(1+1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(0-5\right)^2+\left(1+3\right)^2}=\sqrt{29}\)
=>C=3 căn 5+căn 29

O 1 4 y -4 -1 1 A B C x 2
Tam giác ABC là tam giác vuông
AB=5, BC=6
diện tích tam giác ABC là 5.6:2=15 (dvdt)