Có ai giỏi Hình học ko giúp mình với mai mình thi rồi!
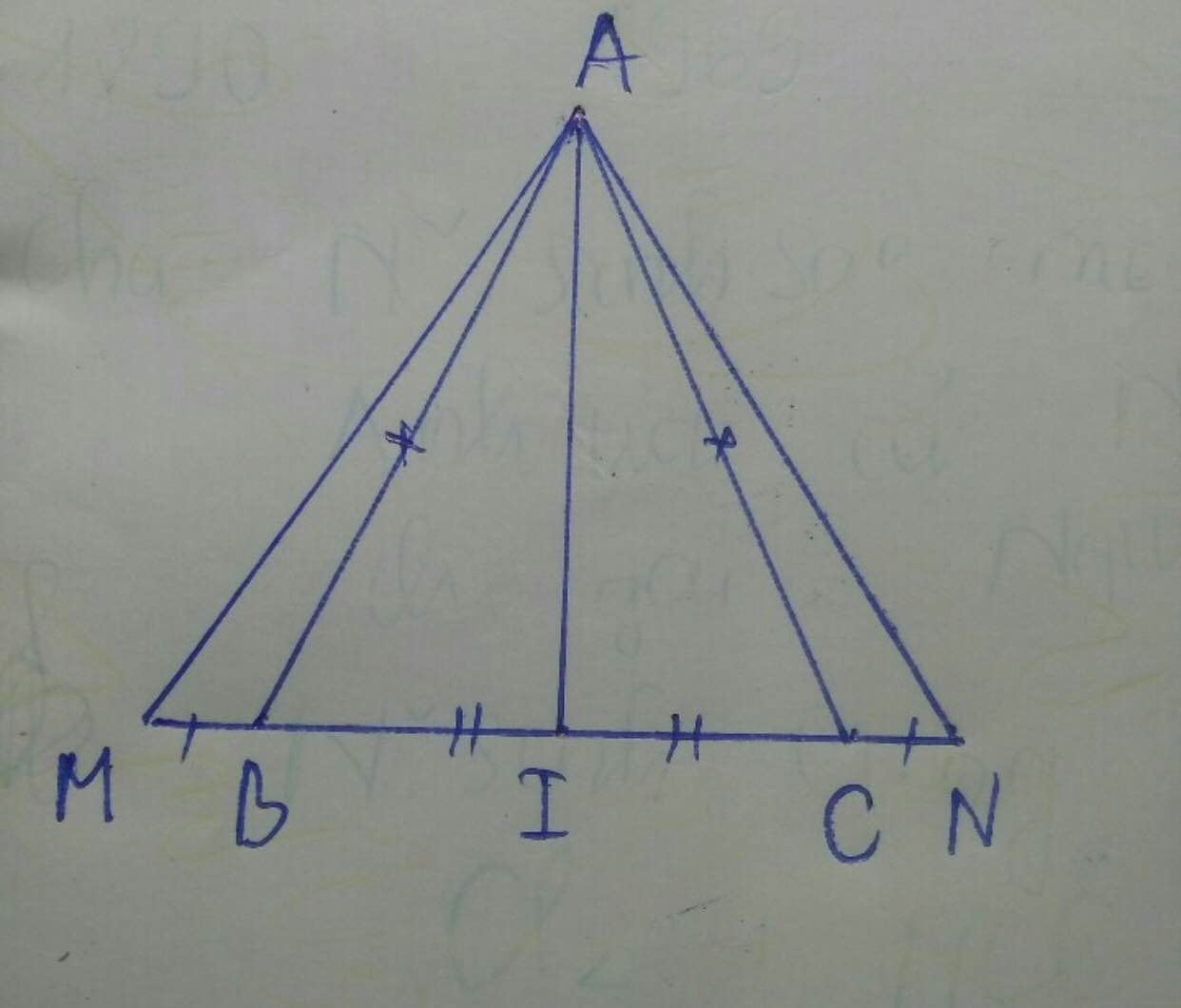
Câu 5: Cho tam giác ABC với AB = AC. Lấy M là trung điểm của BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm K sao cho CN = BK.
a. Chứng minh AM là tia phân giác của ![]()
b. Chứng minh AK = AN
c. Chứng minh AM vuông góc với BC