Bài 1.cho hàm số y= 4/5.x
a)vẽ đồ thị hàm số
b)tìm giá trị của hàm số tại x=(-1);x=0
bài 2. cho hàm số y=-2/5.x
a)vẽ đồ thị hàm số
b)trong các điểm sau đây thì điểm nào thuộc đồ thị hàm số đó:M(-5;2);N(0;3);P(3;hỗn số -1,1/5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
27 tháng 8 2021
c: Thay x=1 và y=-4 vào (d), ta được:
\(m-1+m+3=-4\)
\(\Leftrightarrow2m=-6\)
hay m=-3
5 tháng 2 2022
a) Hàm số đồ thị :
b) \(M(-4;m) \Rightarrow\) \(\begin{cases} x = -4\\y = m \end{cases}\)
Mà \(y = \dfrac{1}{2}x\)
\(\Rightarrow m = y = -4 . \dfrac{1}{2} = -2\)
Vậy \(m = -2 \)
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
CM
27 tháng 12 2017
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
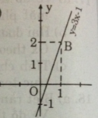
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
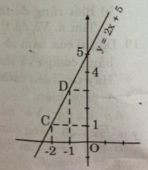
\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
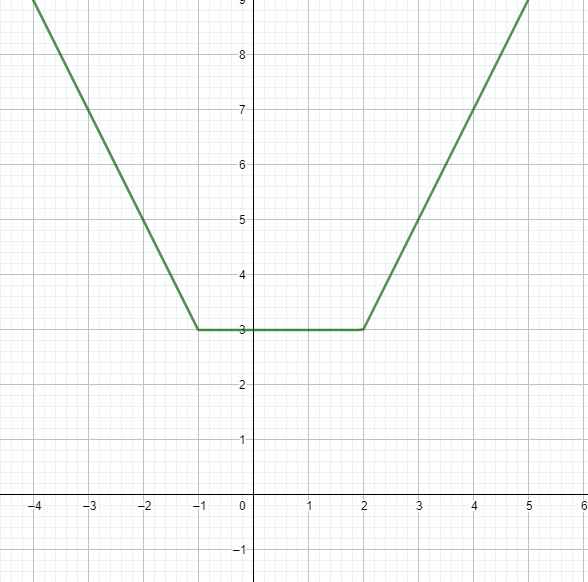
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)
20 tháng 11 2023
1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)