Tìm căn bậc hai của mỗi số phức: -8+6i;3+4i;1-2√2 i
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 11 2019
Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
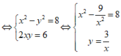
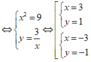
Do đó z có hai căn bậc hai là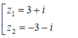 
CM
30 tháng 8 2019
Chọn A.
Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.
Ta có:
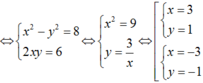
Do đó z có hai căn bậc hai là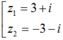 
PT
1
SG
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
Đặt \(\sqrt{8+6i}=x+yi\) với \(x;y\in R\)
\(\Rightarrow8+6i=x^2+2xyi+y^2i^2=x^2-y^2+2xyi\)
\(\Rightarrow\left\{{}\begin{matrix}x^2-y^2=8\\xy=3\end{matrix}\right.\) \(\Rightarrow x^2-\dfrac{9}{x^2}=8\)
\(\Rightarrow x^4-8x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=1\\x=-3\Rightarrow y=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{8+6i}=3+i\\\sqrt{8+6i}=-3-i\end{matrix}\right.\)
PT
1
CM
22 tháng 3 2019
Đáp án D.
Cách 1: Tư duy tự luận
z = − 25 = 25. − 1 = 25 i 2 → z 1,2 = ± 5 i
Cách 2: Sử dụng máy tính cầm tay
Vậy các căn bậc hai của số phức z là z 1,2 = ± 5 i
RH
15 tháng 9 2021
Sqrt(121)=11
Sqrt(144)=12
Sqrt(169)=13
Sqrt(225)=15
Sqrt(256)=16
Sqrt(324)=18
Sqrt(361)=19
Sqrt(400)=20
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
CBHSH:
$\sqrt{121}=11; \sqrt{144}=12; \sqrt{169}=13; \sqrt{225}=15; \sqrt{256}=16; \sqrt{324}=18; \sqrt{361}=19; \sqrt{400}=20$
CBH:
Của $121: \pm 11$
Của $144: \pm 12$
Của $169: \pm 13$
Của $225: \pm 15$
Của $256: \pm 16$
Của $324: \pm 18$
Của $361: \pm 19$
Của $400: \pm 20$