Nếu mắc hai điện trở nối tiếp nhau và vẫn đặt vào 2 đầu đoạn mạch HĐT 24V thì công của dòng điện thay đổi thế nào so với 2 điện trở song song
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
23 tháng 4 2017
Gọi R = R2
Khi mắc song song R t đ 1 = R 1 . R 2 R 1 + R 2 = 2 R 3
Công của dòng điện: A 1 = U . I . t = U 2 R t đ 1 . t = 3 U 2 2 R . t
Khi mắc nối tiếp: R t đ 2 = R 1 + R 2 = 3 R .
Công của dòng điện: A 2 = U 2 R t đ 2 . t = U 2 3 R . t
Ta có: ⇒ A 1 A 2 = 9 2 = 4 , 5 ⇒ A 1 = 4 , 5 A 2
→ Đáp án B
13 tháng 12 2021
\(R_{12}=R_1+R_2=12+36=48\Omega\)
\(I_1=I_2=I=\dfrac{U}{R}=\dfrac{24}{48}=0,5A\)
\(U_1=I_1\cdot R_1=0,5\cdot12=6V\)
\(U_2=U-U_1=24-6=18V\)
\(\left(R_3//R_1\right)ntR_2\)
\(I_m=0,6\Rightarrow R_{tđ}=\dfrac{U}{I}=\dfrac{24}{0,6}=40\Omega\)
\(R_{13}=R-R_2=40-36=4\Omega\)
Ta có: \(\dfrac{1}{R_{12}}=\dfrac{1}{R_1}+\dfrac{1}{R_3}=\dfrac{1}{12}+\dfrac{1}{R_3}=\dfrac{1}{4}\)
\(\Rightarrow R_3=6\Omega\)
VT
11 tháng 10 2018
Điện trở mạch mắc nối tiếp: Rnt = R1 + R2 = 3R1
Vậy U = 0,2.3R1 = 0,6R1
Điện trở mạch mắc song song: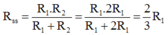
Vậy cường độ dòng điện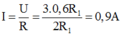 
→ Đáp án D
DN
8 tháng 10 2016
1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
2. a. Theo ht 4' trg đm //, ta có: Rtđ=(R1.R2.R3)/(R1+R2+R3)= (6.12.4)/(6+12+4)=13,09 ôm
b. Áp dụng ĐL Ôm, ta có: U=I.R=3.13,09=39,27 V
c. Theo ĐL Ôm, ta có:
I1=U/R1=39,27/6=6.545 A
I2=U/R2=39,27/12=3,2725 A
I3=U/R3=39,27/4=9.8175 A
23 tháng 10 2021
Bài 1.
\(R_{tđ}=\dfrac{U}{I}=\dfrac{75}{2,5}=30\Omega\)
Có \(R_1ntR_2\Rightarrow R_1+R_2=30\) \(\Rightarrow2R_2+R_2=30\Rightarrow R_2=10\Omega\)
\(\Rightarrow R_1=30-R_2=30-10=20\Omega\)
23 tháng 10 2021
BÀI 2.
Ta có: \(R_{tđ}=\dfrac{U}{I}=\dfrac{45}{2,5}=18\Omega\)
Mà \(R_1//R_2\) \(\Rightarrow\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
Lại có: \(R_1=\dfrac{3}{2}R_2\)
\(\Rightarrow\dfrac{1}{R}=\dfrac{1}{\dfrac{3}{2}R_2}+\dfrac{1}{R_2}=\dfrac{1}{18}\) \(\Rightarrow R_2=30\Omega\)
20 tháng 12 2021
Khi mắc nối tiếp:
\(R_{tđ}=R_1+R_2=\dfrac{U}{I}=\dfrac{24}{0,6}=40\left(\Omega\right)\left(1\right)\)
Khi mắc song song:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12}{1,6}=\dfrac{15}{2}\Rightarrow R_1.R_2=\dfrac{15}{2}.40=300\left(\Omega\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}R_1+R_2=40\left(\Omega\right)\\R_1.R_2=300\left(\Omega\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300}{R_2}+R_2=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300+R_2^2}{R_2}=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\left(R_2-30\right)\left(R_2-10\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}R_1=10\left(\Omega\right)\\R_2=30\left(\Omega\right)\end{matrix}\right.\\\left\{{}\begin{matrix}R_1=30\left(\Omega\right)\\R_2=10\left(\Omega\right)\end{matrix}\right.\end{matrix}\right.\)