Cho hàm số f(x) = sinx. Tính S = f'(x) + f''(x) + f'''(x) +...+ f(2019)(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
QT
1

13 tháng 1 2021
f(x)=4sin2x.cos2x.sinx=4(1-cos2x)cos2x.sinx=(4cos4x-4cos2x)(-sinx)
Đặt u=cosx ---> F(x)=(4/5)cos5x-(4/3)cos3x+C
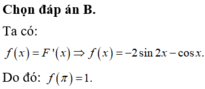
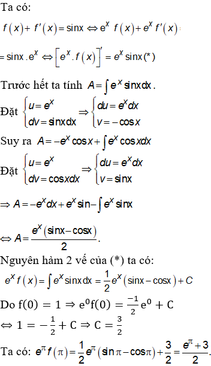
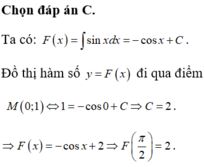


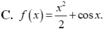

\(f'\left(x\right)=cosx\)
\(f''\left(x\right)=-sinx\)
\(f^{\left(3\right)}\left(x\right)=-cosx\)
\(f^{\left(4\right)}\left(x\right)=sinx\)
Từ đó ta thấy được:
\(f^{\left(4k\right)}\left(x\right)=sinx\)
\(f^{\left(4k+1\right)}\left(x\right)=cosx\)
\(f^{\left(4k+2\right)}\left(x\right)=-sinx\)
\(f^{\left(4k+3\right)}\left(x\right)=-cosx\)
\(\Rightarrow f^{\left(4k\right)}\left(x\right)+f^{\left(4k+1\right)}\left(x\right)+f^{\left(4k+2\right)}\left(x\right)+f^{\left(4k+3\right)}\left(x\right)=0\)
\(\Rightarrow S=f^{\left(2017\right)}\left(x\right)+f^{\left(2018\right)}\left(x\right)+f^{\left(2019\right)}\left(x\right)\)
(Toàn bộ phần tổng đằng trước nhóm thành các cụm 4 số và triệt tiêu)
\(S=f^{\left(4.504+1\right)}\left(x\right)+f^{\left(4.504+2\right)}\left(x\right)+f^{\left(4.504+3\right)}\left(x\right)\)
\(=cosx-sinx-cosx=-cosx\)