Một con lắc đơn có chiều dài = 2,45 m dao động ở nơi có g = 9,8 m/s2. Kéo con lắc lệch cung độ dài 5 cm rồi thả nhẹ cho dao động. Chọn gốc thời gian vật bắt đầu dao dộng. Chiều dương hướng từ vị trí cân bằng đến vị trí có góc lệch ban đầu. Viết phương trình dao động của con lắc đơn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
5 tháng 2 2018
+ Tần số góc của dao động: ω = g l = 9 , 8 2 , 45 = 2 r a d / s
+ Chiều dương hướng từ vị trí cân bằng đến vị trí có góc lệch ban đầu → Vật ở vị trí biên dương
+ Chọn t = 0 lúc vật bắt đầu dao động nên: s = A ⇒ cos φ = 1 ⇒ φ = 0
+ Phương trình dao động: s = 5 sin 2 t + π 2 c m
Chọn đáp án D
VT
5 tháng 1 2019
Tần số góc của dao động
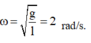
Chiều dương hướng từ vị trí cân bằng đến vị trí góc lệch ban đầu, gốc thời gian lúc vật bắt đầu chuyển động → vật đi qua vị trí cân bằng theo chiều dương →
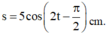
Đáp án C
VT
21 tháng 10 2017
ü Đáp án C
+ Tần số góc của dao động
ω = g l = 2 rad/s
Chiều dương hướng từ vị trí cân bằng đến vị trí góc lệch ban đầu, gốc thời gian lúc vật bắt đầu chuyển động → vật đi qua vị trí cân bằng theo chiều dương → s = 5 cos 2 t - π 2 c m
VT
11 tháng 2 2017
Chọn D.
Chu kì:
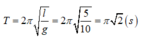
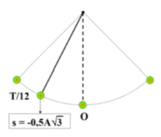
Từ vị trí biên âm sau thời gian t = π 2 / 12 ( s ) = T / 12 thì vật đến li độ s = - A 3 2 .
có vận tốc:
VT
12 tháng 12 2018
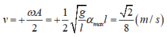
Đáp án C
Tần số góc của dao động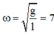 
rad/s.
Gốc thời gian là lúc vật đi qua vị trí có li độ 
theo chiều âm 
Vậy phương trình dao động của vật là α = π 30 cos 7 t + π 3 rad
VT
1 tháng 5 2018
+ Tần số góc của dao động ω = g l = 7 rad/s.
Gốc thời gian là lúc vật đi qua vị trí có li độ α = 30 = 0,5α0 theo chiều âm ⇒ φ 0 = π 3 .
Vậy phương trình dao động của vật là
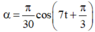rad
Đáp án C
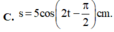
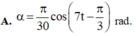
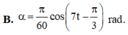
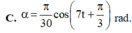
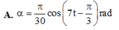
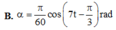
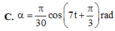
\(S=l.\alpha_0\Rightarrow\alpha_0=\dfrac{5}{245}=\dfrac{1}{49}\left(rad\right)\)
\(\omega=\sqrt{\dfrac{g}{l}}=\sqrt{\dfrac{9,8}{2,45}}=2\left(rad/s\right)\)
Phương trình viết theo li độ góc: \(\alpha=\dfrac{1}{49}\cos\left(2t+\pi\right)\left(rad\right)\)
Phương trình theo li độ dài: \(S=5\cos\left(2t+\pi\right)\left(cm\right)\)