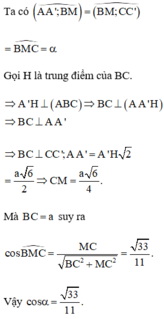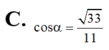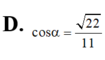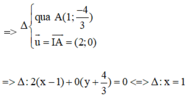Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
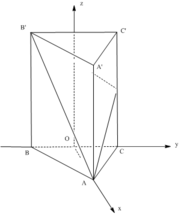
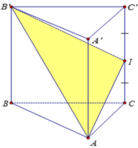
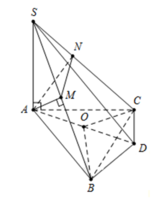
Gắn hệ trục tọa độ Oxyz như hình vẽ
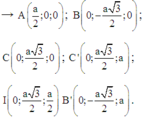
Vecto pháp tuyến của mặt phẳng
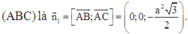
Vecto pháp tuyến của mặt phẳng (AB’I) là
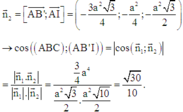

Chọn A
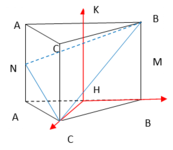
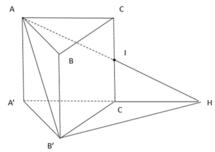
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
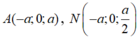
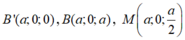
Xét mặt phẳng (BC'N) có
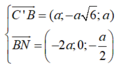
![]()
Phương trình (BC'N) là:
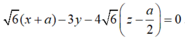
Khoảng cách từ M đến (BC'N) là:
![]()
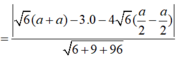


tham khảo
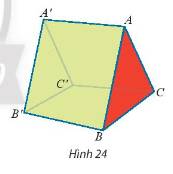
a) Vì \(AA'//BB'\) nên góc giữa \(AA'\) và \(BC\) là góc giữa \(BB'\) và \(BC\).
Vì cạnh bên vuông góc với đáy nên \(BB'\perp BC\). Do đó, \(\widehat{B'BC}=90^o\)
Vì \(A'B'//AB\) nên góc giữa \(A'B'\) và \(AC\) là góc giữa \(AB\) và \(AC\).
Ta có:\(\cos\widehat{BAC}=\dfrac{2,4^2+2,4^2-2^2}{2.2,4.2,4}=\dfrac{47}{72}\)
Nên \(\widehat{BAC}=49,2^o\)
b) Kẻ \(AH\perp BC\). Vì cạnh bên vuông góc với đáy nên \(BB'\perp AH\).
Ta có \(AH\perp BB',AH\perp BC\) nên \(AH\perp\left(BCC'B'\right)\).

Đáp án: C
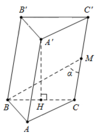
Gọi H là trung điểm BC ⇒ A ' H ⊥ ( A B C )
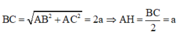
![]()
S ∆ A B C = 1 2 A B . A C = a 2 3 2
Kết luận V = a 3 . a 2 3 2 = 3 a 3 2

Đáp án C
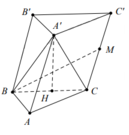
Ta có cos α = cos C C ' ; B M ^ = cos B M C ^ .
Cạnh A ' H = B C 3 2 = a 3 2 , A H = A B 3 2 = a 3 2
A A ' = A ' H 2 + A H 2 = a 6 2 ⇒ M C = a 6 4 .
Cạnh B ' H = A ' B ' 2 + A ' H 2 = a 7 2 .
Do đó cos B ' B H ^ = B B ' 2 + B H 2 - B ' H 2 2 B B ' . B H = 0 ⇒ B ' B ⊥ B H
⇒ M C ⊥ B C ⇒ c o s M B C ^ = M C B M = M C B C 2 + M C 2 = 33 11 .