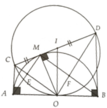
Cho đường tròn (O) và dây AB không là đường kính, C là một điểm trên AB, D là 1 điểm trên cung nhỏ AB của (O), OD cắt AB tại E. đường thẳng OC cắt \(\left(O^,\right)\)ngoại tiếp tam giác OAB tại F, EF cắt \(\left(O^,\right)\)tại G, GD cắt\(\left(O^,\right)\)tại H. Chứng minh:
1) tam giác OCD đồng dạng tam giác ODF từ đó suy ra góc CFD= góc CDO
2)Gọi S là trung điểm của CD. Chứng minh 3 điểm O,H,S thẳng hàng