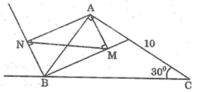
Từ đỉnh A của tam giác ABC ta hạ các đường vuông góc AM, AN với phân giác trong và ngoài tương ứng của góc B, hạ các đường vuông góc AP, AQ với phân giác trong và ngoài tương ứng của góc C Chứng minh 4 điểm M, N, P, Q thẳng...
Đọc tiếp
Từ đỉnh A của tam giác ABC ta hạ các đường vuông góc AM, AN với phân giác trong và ngoài tương ứng của góc B, hạ các đường vuông góc AP, AQ với phân giác trong và ngoài tương ứng của góc C Chứng minh 4 điểm M, N, P, Q thẳng hàng.
chờ tí :)
bẹn tự vẽ hình nhé
Ta có 2 phân giác của hai góc kề bù thì vuông góc với nhau => \(MB\perp BN\)hay \(\widehat{MBN}=1v\);
\(AM\perp BM,AN\perp BN\left(gt\right)\Rightarrow\widehat{AMB}=\widehat{ANB}=1v\)
Như vậy, tứ giác AMBN có 3 góc vuông là hình chữ nhật.
CM tương tự ta có : tứ giác APCQ là hcn
Biết rằng trong 1 hcn hai đường chèo = nhau và cắt nhau tại trung điểm mỗi đường=> đường chéo MN đi qua trung điểm E của AB.
Mặt khác: EB=EN => tam giác EBN cân tại E => góc ABN = ANB
Mà ABN = NBC (gt) => ABN=ANB
tức là MN//BC ( THEO dấu hiệu nhận biết hai đường thẳng song2)
Như vậy MN vừa đi qua trung điểm E của AB lại vừa // với BC nên M,N phải nằm trên đường trung bình EF của tam giác ABC.
Lập luận tương tự ta sẽ có P,Q cũng nằm trên đường trung bình EF của tam giác ABC -> nên chúng thẳng hàng(đpcm)