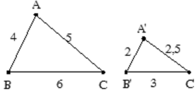
Cho Δ ABC. Vẽ (C; AB); (B; AC). Hai cung này cắt nhau tại D( A; D nằm
trên hai nửa mặt phẳng đối nhau bờ BC). mik cần các bạn cái hình thôi nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

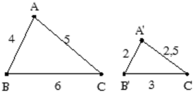
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )

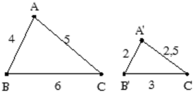
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )

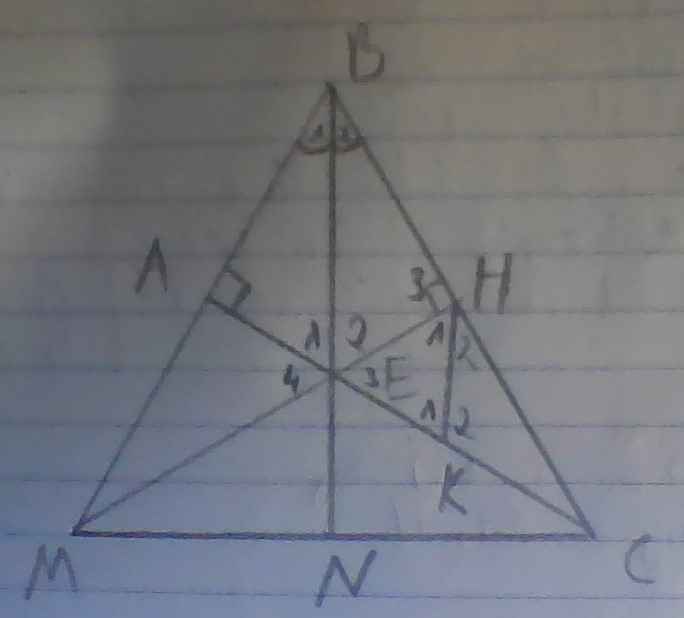
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

Ta có Δ ABC ∼ Δ A'B'C'. Khi đó tỉ số đồng dạng là
A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.

Ta có hình vẽ:
Ta có: ADC + ADB = 180o (kề bù)
=> ADC + 80o = 180o
=> ADC = 180o - 80o = 100o
Vì AD là phân giác của góc A nên \(CAD=DAB=\frac{CAB}{2}\)
Xét Δ ACD có: CAD + ADC + ACD = 180o
=> \(\frac{CAB}{2}\) + 100o + ACD = 180o
=> \(\frac{CAB}{2}\) + ACD = 180o - 100o = 80o (1)
Xét Δ ADB có: ADB + DAB + ABD = 180o
=> 80o + \(\frac{CAB}{2}\) + ABC = 180o
=> \(\frac{CAB}{2}\) + ABC = 180o - 80o = 100o (2)
Từ (1) và (2) \(\Rightarrow\left(\frac{CAB}{2}+ABC\right)-\left(\frac{CAB}{2}+ACD\right)=100^o-80^o\)
=> ABC - ACD = 20o
=> \(\frac{3}{2}ACD-ACD=20^o\)
\(\Rightarrow\frac{1}{2}ACD=20^o\Rightarrow ACD=20^o:\frac{1}{2}=40^o\)
=> ABC = 20o + 40o = 60o
Lại có: ABC + ACD + CAB = 180o
=> 60o + 40o + CAB = 180o
=> 100o + CAB = 180o
=> CAB = 180o - 100o = 80o
Vậy CAB = 80o; ABC = 60o; ACB = ACD = 40o

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}+60^0=90^0\)
hay \(\widehat{C}=30^0\)
Vậy: \(\widehat{C}=30^0\)
a) Xét ΔABC có \(\widehat{C}< \widehat{B}< \widehat{A}\left(30^0< 60^0< 90^0\right)\)
mà cạnh đối diện với góc C là cạnh AB
và cạnh đối diện với góc B là cạnh AC
và cạnh đối diện với góc A là cạnh BC
nên AB<AC<BC(đpcm)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
c: ΔABH vuông tại H
mà HE là đường cao
nên AE*AB=AH^2
ΔACH vuông tại H có HF là đường cao
nên AF*AC=AH^2=AE*AB