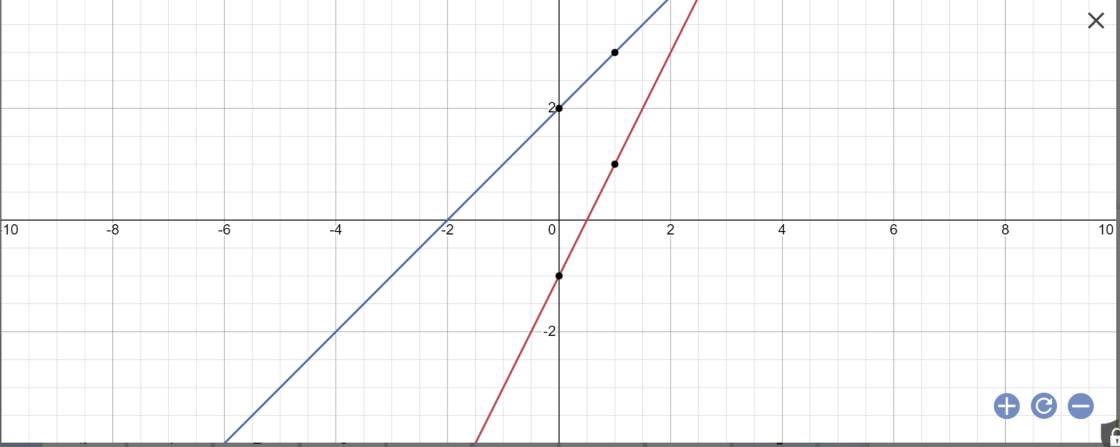
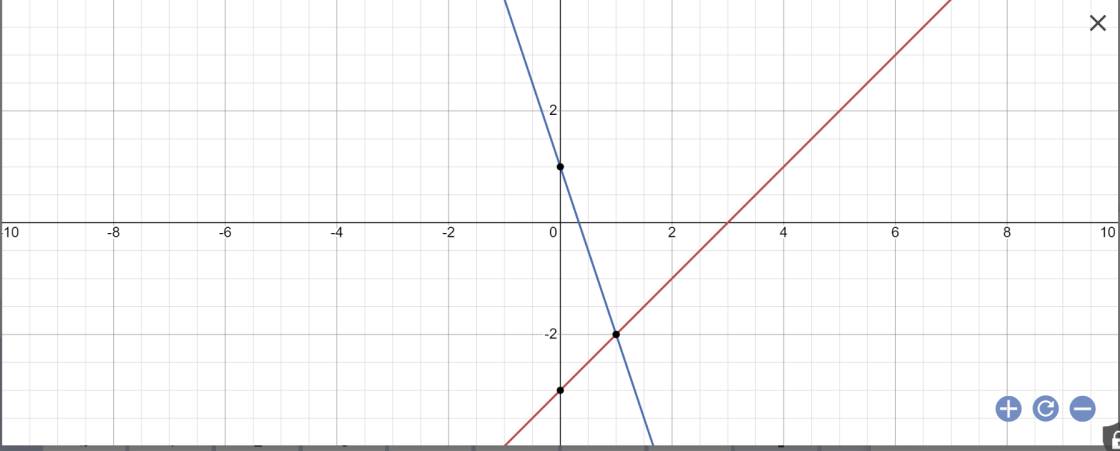
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng \(\left(d_1\right):y=2x+m;\left(d_2\right):y=\left(m^2+1\right)x-1\) (Với m là tham số)
a) Tìm m để d1 cắt Ox ở A, cắt Oy ở B (A và B khác O) sao cho \(AB=2\sqrt{5}\)
b) Tìm tọa độ giao điểm C của d1 và d2 khi m=2