Phân tích đa thức sau thành nhân tử A) 12x³-9x2+3x B) x2-y²+6x+9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3
a) x² + 10x + 25
= x² + 2.x.5 + 5²
= (x + 5)²
b) 8x - 16 - x²
= -(x² - 8x + 16)
= -(x² - 2.x.4 + 4²)
= -(x - 4)²
c) x³ + 3x² + 3x + 1
= x³ + 3.x².1 + 3.x.1² + 1³
= (x + 1)³
d) (x + y)² - 9x²
= (x + y)² - (3x)²
= (x + y - 3x)(x + y + 3x)
= (y - 2x)(4x + y)
e) (x + 5)² - (2x - 1)²
= (x + 5 - 2x + 1)(x + 5 + 2x - 1)
= (6 - x)(3x + 4)
Bài 4
a) x² - 9 = 0
x² = 9
x = 3 hoặc x = -3
b) (x - 4)² - 36 = 0
(x - 4 - 6)(x - 4 + 6) = 0
(x - 10)(x + 2) = 0
x - 10 = 0 hoặc x + 2 = 0
*) x - 10 = 0
x = 10
*) x + 2 = 0
x = -2
Vậy x = -2; x = 10
c) x² - 10x = -25
x² - 10x + 25 = 0
(x - 5)² = 0
x - 5 = 0
x = 5
d) x² + 5x + 6 = 0
x² + 2x + 3x + 6 = 0
(x² + 2x) + (3x + 6) = 0
x(x + 2) + 3(x + 2) = 0
(x + 2)(x + 3) = 0
x + 2 = 0 hoặc x + 3 = 0
*) x + 2 = 0
x = -2
*) x + 3 = 0
x = -3
Vậy x = -3; x = -2

a) \(A=x^2-6x+9-9y^2\)
\(=\left(x-3\right)^2-\left(3y\right)^2\)
\(=\left(x-3-3y\right)\left(x-3+3y\right)\)
b) \(B=x^3-3x^2+3x-1+2\left(x^2-1\right)\)
\(=\left(x-1\right)^3+\left(2x+2\right)\left(x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)^2+2x+2\right]\)
\(=\left(x-1\right).\left(x^2+3\right)\)
a, \(A=\left(x-3\right)^2-9y^2=\left(x-3-3y\right)\left(x-3+3y\right)\)
b, \(B=\left(x-1\right)^3+2\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left[\left(x-1\right)^2+2\left(x+1\right)\right]\)
\(=\left(x-1\right)\left(x^2-2x+1+2x+2\right)=\left(x-1\right)\left(x^2+3\right)\)

Bài `1`
\(a,5x^2-10xy=5x\left(x-2y\right)\\ b,3x\left(x-y\right)-6\left(x-y\right)=\left(x-y\right)\left(3x-6\right)\\ =3\left(x-y\right)\left(x-2\right)\\ c,2x\left(x-y\right)-4y\left(y-x\right)=2x\left(x-y\right)+4y\left(x-y\right)\\ =\left(x-y\right)\left(2x+4y\right)=2\left(x-y\right)\left(x+2y\right)\\ d,9x^2-9y^2=\left(3x\right)^2-\left(3y\right)^2=\left(3x-3y\right)\left(3x+3y\right)\\ f,xy-xz-y+z=\left(xy-xz\right)-\left(y-z\right)\\ =x\left(y-z\right)-\left(y-z\right)=\left(y-z\right)\left(x-1\right)\)
Bài `3`
\(a,3x^2+8x=0\\ \Leftrightarrow x\left(3x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x=-8\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{8}{3}\end{matrix}\right.\)
\(b,9x^2-25=0\\ \Leftrightarrow\left(3x\right)^2-5^2=0\\ \Leftrightarrow\left(3x-5\right)\left(3x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-5=0\\3x+5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=5\\3x=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(c,x^3-16x=0\\ \Leftrightarrow x\left(x^2-16\right)=0\\ \Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
\(d,x^3+x=0\\ \Leftrightarrow x\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1\in\varnothing\\x=0\end{matrix}\right.\Rightarrow x=0\)

Lời giải:
a. $5x^2-10xy=5x(x-2y)$
b. $3x(x-y)-6(x-y)=(x-y)(3x-6)=3(x-y)(x-2)$
c. $2x(x-y)-4y(y-x)=2x(x-y)+4y(x-y)=(x-y)(2x+4y)=2(x-y)(x+2y)$
d. $9x^2-9y^2=9(x^2-y^2)=9(x-y)(x+y)$
e. $x^2-xy-x+y=(x^2-xy)-(x-y)=x(x-y)-(x-y)=(x-y)(x-1)$
f. $xy-xz-y+z=(xy-y)-(xz-z)=y(x-1)-z(x-1)=(x-1)(y-z)$

1b.=2((x+y)+(x+y)(x-y)+(x-y))=2(x2-y2+x+y+x-y)=2(x2-y2+2x)=2x2-2y2+4x
2a.=4xy+4xy+2y=8xy+2y=2y(4x+1)
b.=(3x)2+2.3x.y+y2-(2z)2=(3x+y)2-(2z)2=(3x+y-2z)(3x+y+2z)
c.=x2-x-7x+7=x(x-1)-7(x-1)=(x-1)(x-7)
\(\left(x+y\right)^2+2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
hk tốt
^^

`1)x^3-7x+6`
`=x^3-x-6x+6`
`=x(x-1)(x+1)-6(x-1)`
`=(x-1)(x^2+x-6)`
`=(x-1)(x^2-2x+3x-6)`
`=(x-1)[x(x-2)+3(x-2)]`
`=(x-1)(x-2)(x+3)`
`2)x^3-9x^2+6x+16`
`=x^3-2x^2-7x^2+14x-8x+16`
`=x^2(x-2)-7x(x-2)-8(x-2)`
`=(x-2)(x^2-7x-8)`
`=(x-2)(x^2-8x+x-8)`
`=(x-2)[x(x-8)+x-8]`
`=(x-2)(x-8)(x+1)`
`3)x^3-6x^2-x+30`
`=x^3+2x^2-8x^2-16x+15x+30`
`=x^2(x+2)-8x(x+2)+15(x+2)`
`=(x+2)(x^2-8x+15)`
`=(x+2)(x^2-3x-5x+15)`
`=(x+2)[x(x-3)-5(x-3)]`
`=(x+2)(x-3)(x-5)`
`4)2x^3-x^2+5x+3`
`=2x^3+x^2-2x^2-x+6x+3`
`=x^2(2x+1)-x(2x+1)+3(2x+1)`
`=(2x+1)(x^2-x+3)`
`5)27x^3-27x^2+18x-4`
`=27x^3-9x^2-18x^2+6x+12x-4`
`=9x^2(3x-1)-6x(3x-1)+4(3x-1)`
`=(3x-1)(9x^2-6x+4)`
1) Ta có: \(x^3-7x+6\)
\(=x^3-x-6x+6\)
\(=x\left(x^2-1\right)-6\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-6\right)\)
\(=\left(x-1\right)\left(x+3\right)\left(x-2\right)\)
2) Ta có: \(x^3-9x^2+6x+16\)
\(=x^3-2x^2-7x^2+14x-8x+16\)
\(=x^2\left(x-2\right)-7x\left(x-2\right)-8\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2-7x-8\right)\)
\(=\left(x-2\right)\left(x-8\right)\left(x+1\right)\)
3) Ta có: \(x^3-6x^2-x+30\)
\(=x^3+2x^2-8x^2-16x+15x+30\)
\(=x^2\left(x+2\right)-8x\left(x+2\right)+15\left(x+2\right)\)
\(=\left(x+2\right)\left(x^2-8x+15\right)\)
\(=\left(x+2\right)\left(x-3\right)\left(x-5\right)\)
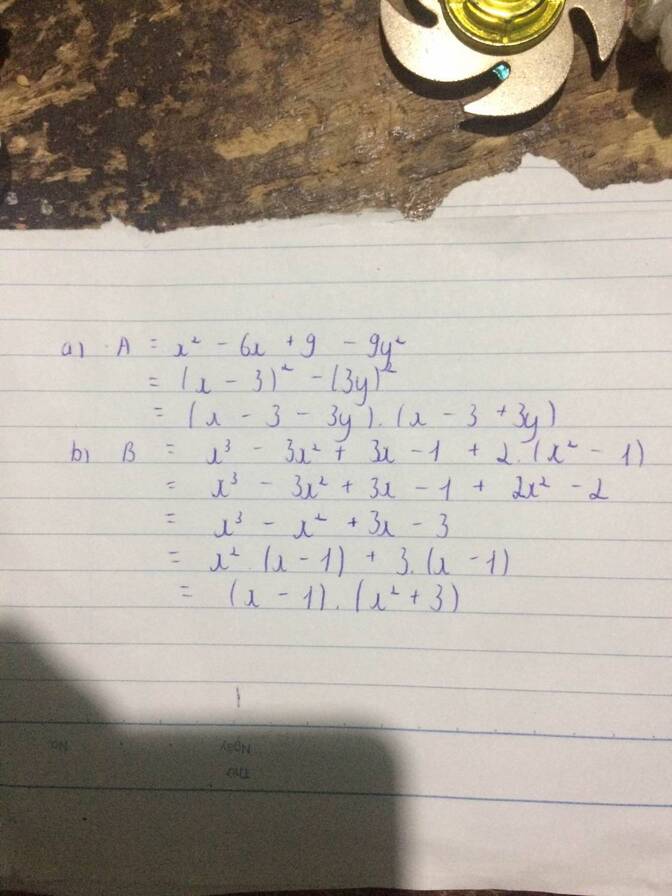
a ) x=0; x = -(căn bậc hai(7)*i-3)/8;x = (căn bậc hai(7)*i+3)/8;
b ) -(y-x-3)*(y+x+3)
a) \(12x^3-9x^2+3x\)
\(=3x\left(4x^2-3x+1\right)\)
b) \(x^2-y^2+6x+9\)
\(=\left(x^2+6x+9\right)-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+y+3\right)\left(x-y+3\right)\)