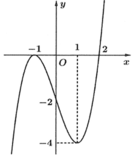
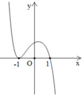
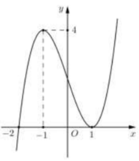
Cho hàm số y = f(x) liên tục trên ℝ . Đồ thị của hàm số y=f '(x) như hình bên. Đặt g x = 2 f x − x + 1 2 . Mệnh đề nào dưới đây đúng?
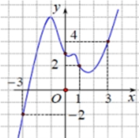
A. min − 3 ; 3 g x = g 1 .
B. max − 3 ; 3 g x = g 1 .
C. min − 3 ; 3 g x = g 3 .
D. Không tồn tại giá trị nhỏ nhất của g(x) trên − 3 ; 3 .

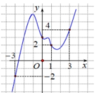
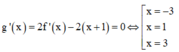
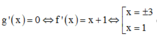








Đáp án là B