Phương trình đường thẳng song song với đường thẳng d : x − 1 1 = y + 2 1 = z − 1 và cắt hai đường thẳng d 1 : x + 1 2 = y + 1 1 = z − 2 − 1 và d 2 : x − 1 − 1 = y − 2 1 = z − 3 3 là
A. x + 1 − 1 = y + 1 − 1 = z − 2 1
B. x − 1 1 = y 1 = z − 1 − 1
C. x − 1 1 = y − 2 1 = z − 3 − 1
D. x − 1 1 = y − 1 = z − 1 1

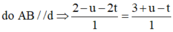
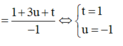
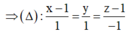
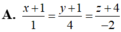
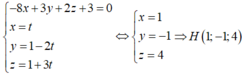

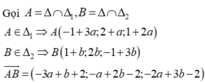
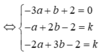
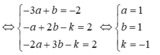
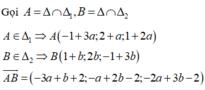

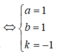




Đáp án là B