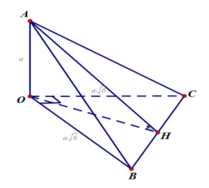
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và A B = O C = a 6 , O A = a . Tính góc giữa hai mặt phẳng (ABC) và (OBC)
A. 60 °
B. 30 °
C. 45 °
D. 90 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2018
Đáp án là A
Trong (OBC) kẻ OH ⊥ BC tại H thì có ngay BC ⊥ (OAH)
Do đó :
(vì tam giác OHA vuông tại O nên A H O ^ < 90 o )
Ta có
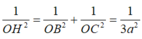
Ta giác OHA vuông tại O nên
Vậy góc giữa hai mặt phẳng (ABC) và (OBC) bằng 30 o
CM
6 tháng 10 2017
Đáp án A
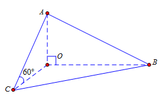
Theo giả thiết OA, OB, OC đôi một vuông góc với nhau nên O A ⊥ O B C , O C là hình chiếu của AC lên mặt phẳng O B C . Do đó, A C O ^ = 60 ° , O A là chiều cao của tứ diện OABC. Xét tam giác vuông AOC có tan 60 ° = O A O C với O A = a ⇒ O C = O A tan 60 ° = a 3 = a 3 3 ; O B = 2 a
Ta có S O B C = 1 2 O B . O C = 1 2 2 a . a 3 3 ; V O A B C = 1 3 O A . S O B C = 1 3 a . a 2 3 3 = a 3 3 9
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
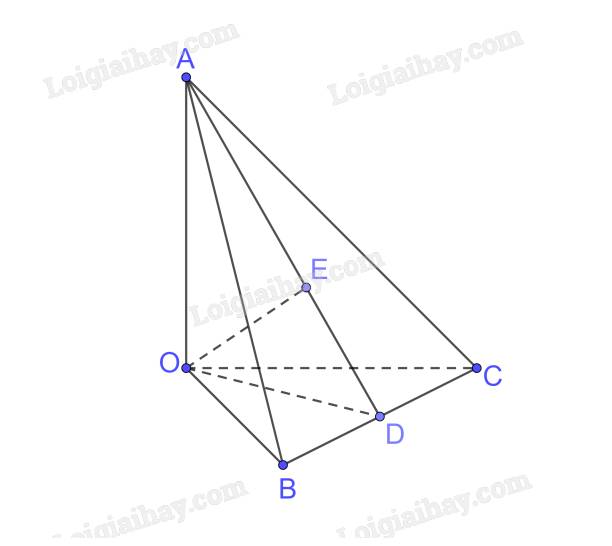
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)
CM
10 tháng 3 2017
Đáp án D
Gọi H là hình chiếu của O xuống (ABC)
Ta có: 1 O H 2 = 1 a 2 + 1 2 a 2 + 1 a 3 2 = 19 12 a 2 ⇒ O H = 2 a 3 19
Đáp án B