Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
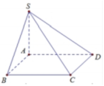
A. SDA
B. SCA
C. SCB
D. ASD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2019
Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Đáp án A.
Phương pháp:
Xác định góc giữa hai mặt phẳng α , β :
- Tìm giao tuyến Δ của α , β .
- Xác định 1 mặt phẳng γ ⊥ Δ .
- Tìm các giao tuyến a = α ∩ γ , b = β ∩ γ
- Góc giữa hai mặt phẳng α , β : α ; β = a ; b .
Cách giải:
Ta có: S C D ∩ A B C D = C D
Mà C D ⊥ A D (ABCD là hình vuông), C D ⊥ S A (vì S A ⊥ A B C D ) ⇒ C D ⊥ S A D
S C D ∩ S A D = S D ,
A B C D ∩ S A D = A D ⇒ S C D , A B C D = S D ; A D = S D A