Chọn câu đúng trong các câu sau:
Tứ giác ABCD có thể có 4 góc đều là góc nhọn.
Tứ giác ABCD có thể có 4 góc đều là góc tù.
Tứ giác ABCD có thể có 2 góc vuông và 2 góc tù.
Tứ giác ABCD có thể có 4 góc đều là góc vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Nếu cả bốn góc trong một tứ giác đều là góc nhọn thì tổng của bốn góc đó sẽ nhỏ hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
Nếu cả bốn góc trong một tứ giác đều là góc tù thì tổng của bốn góc đó sẽ lớn hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
Ta có đpcm
1) Xét ΔABC và ΔCDA có
AB=CD(gt)
\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, AB//CD)
AC chung
Do đó: ΔABC=ΔCDA(c-g-c)
Suy ra: \(\widehat{ACB}=\widehat{CAD}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC(Đpcm)

Đáp án A.
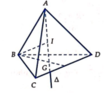
Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất
![]()
![]()
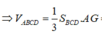
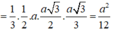

Đáp án A.
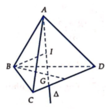
Gọi I là tâm mặt cầu ngoại tiếp ABCD ⇒ I ∈ Δ và I A = I B = R
Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất <=> IB nhỏ nhất
⇔ I B ⊥ Δ ⇔ I ≡ G ⇒ I A = I B = B G = a 3 3 = A G ⇒ V A B C D = 1 3 S B C D . A G = 1 3 . 1 2 . a . a 3 2 . a 3 3 = a 2 12

Đáp án C
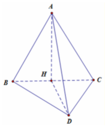
Gọi H là trung điểm của BC. Ta có: A H ⊥ B C
Mặt khác A B C ⊥ B C D ⇒ A H ⊥ B C D
Lại có A H = a 3 2 ⇒ V = 1 3 A H . S B C D = 1 3 . a 3 2 . a 2 3 4 = a 3 8