Tìm số đo ba góc của một tam giác cân, biết rằng số đo của một góc là nghiệm của phương trình c o s 2 x = − 1 2
A. 2 π 3 , π 6 , π 6 .
B. π 3 , π 3 , π 3 .
C. π 3 , π 3 , π 3 ; π 4 , π 4 , π 2 .
D. π 3 , π 3 , π 3 ; 2 π 3 , π 6 , π 6 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Giải phương trình cos 2 x = - 1 2 , tính được 1 góc và suy ra các góc còn lại của tam giác cân.
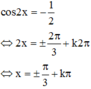
Vì x là số đo của 1 góc của tam giác cân nên
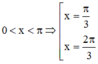
Với x = π 3 ⇒ tam giác cân trở thành tam giác đều => 3 góc của tam giác là π 3 ; π 3 ; π 3
Với x = 2 π 3 ⇒ 2 góc còn lại của tam giác cân đều bằng π 6 ⇒ 3 góc của tam giác là 2 π 3 ; π 6 ; π 6

Gọi số đo góc thứ nhất là 2x.
=> số đo góc thứ hai là 3x, số đo góc thứ ba là 4x.
Tổng 3 góc trong 1 tam giác là 180 độ.
=> 2x + 3x + 4x = 180. => 9x = 180. => x = 20.
Vậy số đo góc thứ nhất là 2x = 2.20 = 40 độ; số đo góc thứ hai là 3x = 3.20 = 60 độ; số đo góc thứ ba là 4x = 4.20 = 80 độ.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{1}=\dfrac{b}{\dfrac{3}{2}}=\dfrac{c}{2}=\dfrac{a+b+c}{1+\dfrac{3}{2}+2}=\dfrac{180}{\dfrac{9}{2}}=40\)
Do đó: a=40; b=60; c=80
Đáp án là D