Cho hai số phức z 1 , z 2 thỏa mãn z 1 = z 2 = 17 . Gọi M, N lần lượt là các điểm biểu diễn z 1 , z 2 trên mặt phẳng tọa độ. Biết M N = 3 2 , gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của ON. Tính l = K H .
A. l = 17 2 .
B. l = 5 2 .
C. l = 3 13 2 .
D. l = 5 2 2 .



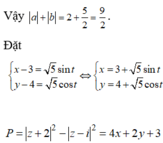
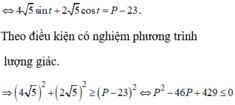
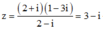
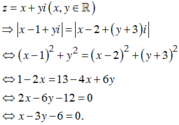
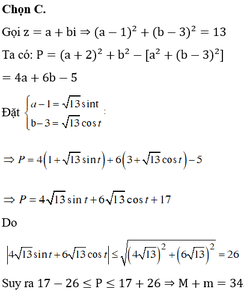
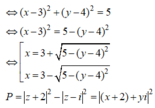
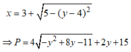

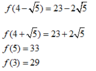
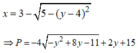
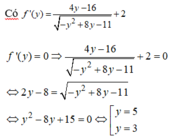
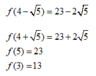
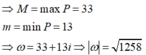
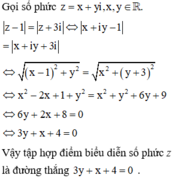

Đáp án C.
Ghi nhớ: Công thức đường trung tuyến:
m a 2 = b 2 + c 2 2 − a 2 4 .
Gọi E là giao điểm của OH và MN.
Ta có:
O E 2 = O M 2 + O N 2 2 − M N 2 4 = 17 − 9 2 = 25 2 ⇒ O H 2 = 50.
H K 2 = H N 2 + H O 2 2 − O N 2 4 = O M 2 + O H 2 2 − O N 2 4 = 17 + 50 2 − 17 4 = 117 4 ⇒ H K = 3 13 2 .