Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = x + 1 x trên đoạn 1 ; 4 là
A. 2
B. 17 2
C. 17 4
D. 28 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
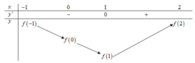
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()

\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)

Chọn A
Ta có: ![]()
![]()
![]()
![]()
![]()
![]()
Với ![]() nên f(x) đồng biến trên
ℝ
nên f(x) đồng biến trên
ℝ
Với ![]() nên f(x) nghich biến trên
ℝ
nên f(x) nghich biến trên
ℝ
Suy ra: ![]() Vì f(x) nghich biến trên
ℝ
nên
Vì f(x) nghich biến trên
ℝ
nên 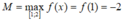 và
và ![]()
Từ đây ,ta suy ra: ![]()
=> chọn đáp án A
Đáp án B
Ta có: f ' x = 1 − 1 x 2 = x 2 − 1 x 2 ≥ 0 ∀ x ∈ 1 ; 4 do đó hàm số đồng biến trên đoạn 1 ; 4
Do đó M i n 1 ; 4 f x . M ax 1 ; 4 f x = f 1 . f 4 = 17 2 .