Cho các số thực a < b < 0 . Mệnh đề nào sau đây là sai ?
A. ln a b = 1 2 ln a + ln b
B. ln a b = ln a − ln b
C. ln a b 2 = ln a 2 − ln b 2
D. ln a b 2 = ln a 2 + ln b 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


Đáp án B
Đặt 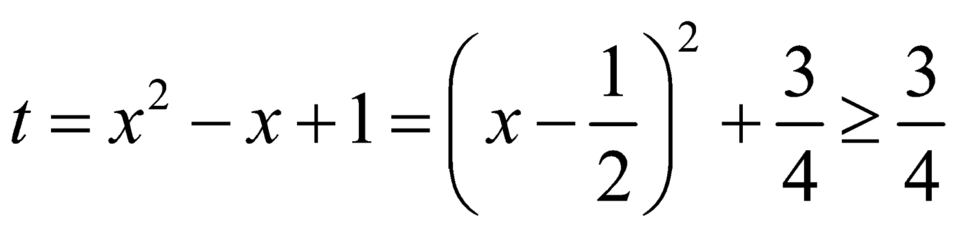
Ta có:
![]()
![]()
Đặt ![]() .
.
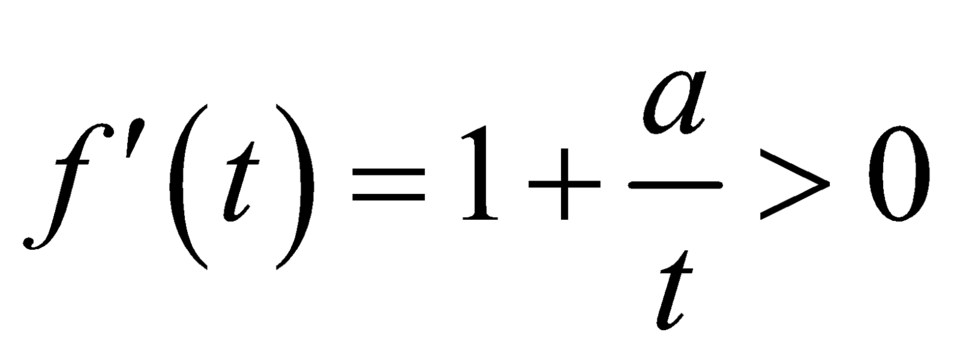
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 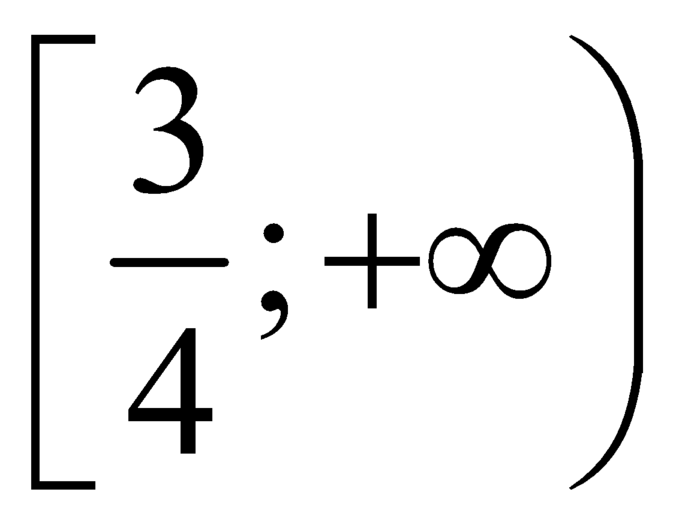 .
.
Khi đó 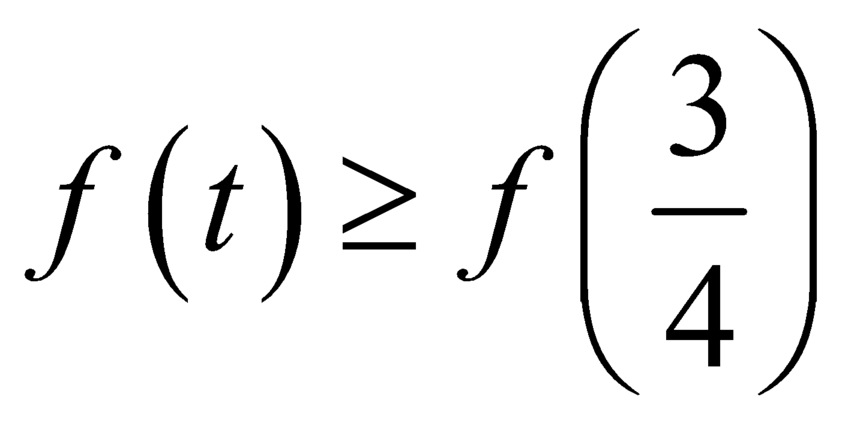
![]()
![]()
![]()

\(a,A=ln\left(\dfrac{x}{x-1}\right)+ln\left(\dfrac{x+1}{x}\right)-ln\left(x^2-1\right)\\ =ln\left(\dfrac{x}{x-1}\cdot\dfrac{x+1}{x}\right)-ln\left(x^2-1\right)\\ =ln\left(\dfrac{x+1}{x-1}\right)-ln\left(x^2-1\right)\\ =ln\left(\dfrac{x+1}{x-1}\cdot\dfrac{1}{x^2-1}\right)\\ =ln\left[\dfrac{1}{\left(x-1\right)^2}\right]\\ =2ln\left(\dfrac{1}{x-1}\right)\)
\(b,21log_3\sqrt[3]{x}+log_3\left(9x^2\right)-log_3\left(9\right)\\ =7log_3\left(x\right)+log_3x^2+log_39-log_39\\ =7log_3x+2log_3x\\ =9log_3x\)

a)
\(\begin{array}{c}A = {\log _{\frac{1}{3}}}5 + 2{\log _9}25 - {\log _{\sqrt 3 }}\frac{1}{5} = {\log _{{3^{ - 1}}}}5 + 2{\log _{{3^2}}}{5^2} - {\log _{{3^{\frac{1}{2}}}}}{5^{ - 1}}\\ = - {\log _3}5 + 2{\log _3}5 + 2{\log _3}5 = 3{\log _3}5\end{array}\)
b) \(B = {\log _a}{M^2} + {\log _{{a^2}}}{M^4} = 2{\log _a}M + \frac{1}{2}.4{\log _a}M = 4{\log _a}M\)

a) Bất phương trình đã cho tương đương với hệ sau:
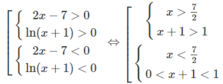
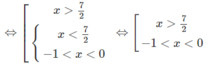
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
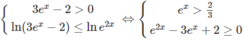
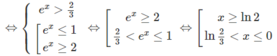
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
Đáp án A
Ta có: ln a b = 1 2 ln a + ln b là khẳng định sai vì a < b < 0.