Cho hình chóp S.ABC có ABC là tam giác vuông tại B, A B = a , B C = 2 a . Biết S A ⊥ A B , S C ⊥ B C , góc giữa SC và (ABC) bằng 60 0 . Độ dài cạnh SB bằng:
A. 2 a
B. 2 2 a
C. 3 a
D. 3 2 a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

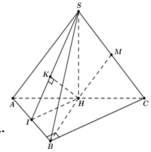
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
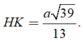

Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
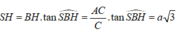
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2

Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)

Đáp án C
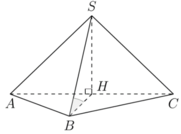
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12

Qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại D
\(\left\{{}\begin{matrix}SC\perp\left(ABC\right)\Rightarrow SC\perp CD\\CD\perp AC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAC\right)\)
Kẻ \(CH\perp SB\Rightarrow CH\perp\left(SAB\right)\)
\(\Rightarrow\widehat{HCD}\) là góc giữa (SAB) và (SAC)
\(BC=\sqrt{AC^2-AB^2}=a\sqrt{2}\)
\(\dfrac{1}{CH^2}=\dfrac{1}{SC^2}+\dfrac{1}{BC^2}=\dfrac{13}{24a^2}\Rightarrow CH=\dfrac{2a\sqrt{78}}{13}\)
\(CD=AC.tanA=AC.\dfrac{BC}{AB}=a\sqrt{6}\)
\(sin\widehat{HCD}=\dfrac{DH}{CD}=\dfrac{\sqrt{CD^2-CH^2}}{CD}=...\)
Đáp án B
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .