Cho a,b,c là các số thực thuộc đoạn
1
;
2
thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức
P
=
a
3
+
b
3
+
c
3
−
3
log
2
a
a
+
log
2
b
b
+
log
2
c
c
đạt giá trị lớn nhất thì giá trị của tổng
a
+
b
+
c
là:
A. 3
B. 3.2 1 3 3
C. 4
D. 6

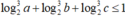 . Khi biểu thức
. Khi biểu thức 



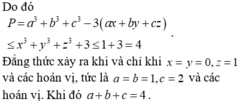
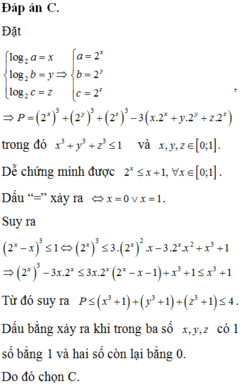

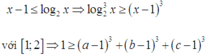
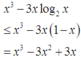
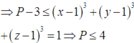
Đáp án C.
Đặt log 2 a = x log 2 b = y log 2 c = z ⇒ a = 2 x b = 2 y c = 2 z ⇒ P = 2 x 3 + 2 y 3 + 2 z 3 − 3 x .2 x + y .2 y + z .2 z ,
trong đó x 3 + y 3 + z 3 ≤ 1 và x , y , z ∈ 0 ; 1 .
Dễ chứng minh được 2 x ≤ x + 1 , ∀ x ∈ 0 ; 1 . Dấu “=” xảy ra ⇔ x = 0 ∨ x = 1 .
Suy ra
2 x − x 3 ≤ 1 ⇔ 2 x 3 ≤ 3. 2 x 2 . x − 3.2 x . x 2 + x 3 + 1 ⇒ 2 x 3 − 3 x .2 x ≤ 3 x .2 x 2 x − x − 1 + x 3 + 1 ≤ x 3 + 1 Từ đó suy ra P ≤ x 3 + 1 + y 3 + 1 + z 3 + 1 ≤ 4 .
Dấu bằng xảy ra khi trong ba số x , y , z có 1 số bằng 1 và hai số còn lại bằng 0. Do đó chọn C.