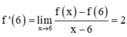Cho hàm số y = f(x) có đạo hàm thỏa mãn f’(6) = 2. Giá trị biểu thức lim x → 6 f ( x ) - f ( 6 ) x - 6 bằng:
A. 2
B. 1/3
C. 1/2
D. 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ L'Hospital:
\(=\lim\limits_{x\rightarrow6}f'\left(x\right)=f'\left(6\right)=2\)
3/ \(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{3}{2\sqrt{3x+3}}}{1}=\dfrac{1}{2}\Rightarrow2a-b=0\)
4/ \(=\lim\limits_{x\rightarrow1}\dfrac{2f\left(x\right).f'\left(x\right)-f'\left(x\right)}{\dfrac{1}{2\sqrt{x}}}=\dfrac{2.6.5-5}{\dfrac{1}{2}}=110\)
2/ \(x_0=-3\Rightarrow y_0=\dfrac{-3-1}{-3+2}=\dfrac{-4}{-1}=4\)
\(y'=\dfrac{\left(x-1\right)'\left(x+2\right)-\left(x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}=\dfrac{x+2-x+1}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)
\(\Rightarrow y'\left(-3\right)=3\)
\(\Rightarrow pttt:y=3\left(x+3\right)+4=3x+13\)
\(x=0\Rightarrow y=13;y=0\Rightarrow x=-\dfrac{13}{3}\)
\(\Rightarrow S=\dfrac{1}{2}.\left|x\right|\left|y\right|=\dfrac{1}{2}.\dfrac{13}{3}.13=\dfrac{169}{6}\left(dvdt\right)\)
P/s: Câu 5,6 bỏ qua nhé, toi ngu hình học :b

\(2x.f'\left(x\right)-f\left(x\right)=x^2\sqrt{x}.cosx\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x}}.f'\left(x\right)-\dfrac{1}{2x\sqrt{x}}f\left(x\right)=x.cosx\)
\(\Leftrightarrow\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'=x.cosx\)
Lấy nguyên hàm 2 vế:
\(\int\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'dx=\int x.cosxdx\)
\(\Rightarrow\dfrac{f\left(x\right)}{\sqrt{x}}=x.sinx+cosx+C\)
\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx+C.\sqrt{x}\)
Thay \(x=4\pi\)
\(\Rightarrow0=4\pi.\sqrt{4\pi}.sin\left(4\pi\right)+\sqrt{4\pi}.cos\left(4\pi\right)+C.\sqrt{4\pi}\)
\(\Rightarrow C=-1\)
\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx-\sqrt{x}\)

Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
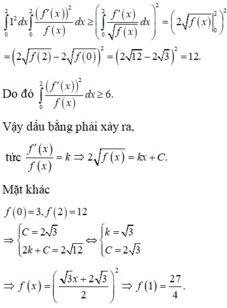
Đáp án A

Đáp án D
∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x = k ≠ 0
Đặt
u = e x d v = f ' x d x ⇒ d u = e x d x v = f x ⇒ ∫ 0 1 e x f ' x d x = e x f x 0 1 − ∫ 0 1 e x f x d x
⇒ k = e . f 1 − f 0 − k ⇒ e f 1 − f 0 = 2 k .
Đặt
u = e x d v = f ' ' x d x ⇒ d u = e x d x v = f ' x ⇒ ∫ 0 1 e x f ' ' x d x = e x f ' x 0 1 − ∫ 0 1 e x f ' x d x
⇒ k = e . f ' 1 − f ' 0 − k ⇒ e . f ' 1 − f ' 0 = 2 k .
Vậy e . f ' 1 − f ' 0 e . f 1 − f 0 = 2 k 2 k = 1
Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm bằng định nghĩa: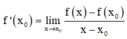 (nếu tồn tại giới hạn).
(nếu tồn tại giới hạn).
Cách giải: Ta có: