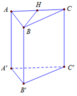
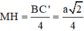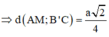Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là:
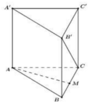
A. a 2 2
B. a 2 4
C. a
D. a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2

Đáp án B

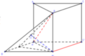
Phương pháp: Dựa vào khoảng cách giữa đường thẳng và mặt phẳng song song tính khoảng cách giữa hai đường thẳng chéo nhau.
+) Lấy mặt phẳng (P) chứa đường thẳng d 2 và song song với d 1
Khi đó d( d 1 , d 2 ) = d( d 1 ,(P))
(Chọn sao cho ta dễ dàng tính được khoảng cách).
+) Tính khoảng cách giữa đường thẳng d 2 và mặt phẳng (P).
Cách giải:
Dựng hình bình hành A’C’B’D
=>A’D//B’C’ => B’C’//(BDA’)
=>D(B’C’;BA’) = d(B’C’;(BDA’))
Gọi J là trung điểm A’D.
Kẻ B’H ⊥ BJ, H ∈ BJ
∆A’B’C’ đều => ∆A’B’D’ đều => B’J ⊥ A’D
Mà BB’ ⊥ A’D => A’D ⊥ (BA’D) => A’D ⊥ B’H
B’H ⊥ (A’DB) => d(B’C;A’B) = B’H
∆A’B’D’ đều, cạnh bằng a => B'J = a 3 2
∆JB’B vuông tại B’ 
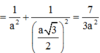
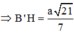
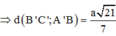

Đáp án D
Gọi P là trung điểm cạnh BC
![]()
Tam giác MPN vuông tại P có
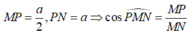
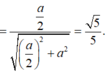

Đáp án D
Ta có B H A C B B ' ⊥ A B C ⇒ B B ' ⊥ B H ⇒ d A C ; B B ' = B H = A B 3 2 = a 3 2
Đáp án B
Phương pháp : Dụng đường vuông góc chung.
Cách giải :
Ta có: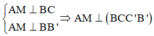
Trong (BCC’B’) kẻ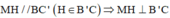
=>MH là đoạn vuông góc chung giữa AM và B’C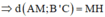
Dễ thấy