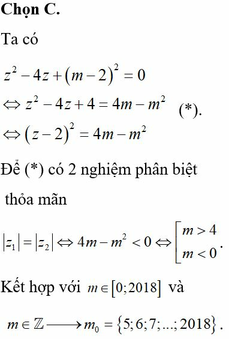Trong tập các số phức, cho phương trình z 2 - 6 z + m = 1 , m∈R (1). Gọi m 0 là một giá trị của m để phương trình (1) có hai nghiệm phân biệt x m 0 thỏa mãn z 1 z 1 ¯ = z 2 z 2 ¯ . Hỏi trong khoảng (0;20) có bao nhiêu giá trị m
A. 13
B. 11
C. 12
D. 10