Cho hàm số y = log 2018 1 x có đồ thị C 1 và hàm số y = f x có đồ thị C 2 Biết C...

PT

Pham Trong Bach

8 tháng 3 2018

Cho hàm số y = log 2018 1 x có đồ thị C 1 và hàm số y = f x có đồ thị C 2 Biết C 1 và C 2 đối xứng nhau qua gốc tọa độ. Hỏi hàm số y = f x nghịch biến trên khoảng nào sau đây A. - ∞ ; - 1 B. - 1 ; 0 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

8 tháng 3 2018

Đúng(0)

PT

Pham Trong Bach

24 tháng 5 2019

Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y=f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ? A. 24. B. 28. C. 26. D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

24 tháng 5 2019

Ta có đạo hàm : f’ (x) = 3ax²+ 2bx+ c.

Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0

+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.

Suy ra: f’(x) = 3x²+ 2 và f( x) = x³+ 2x+ d,

+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d

Suy ra: d= 0.

Khi đó ta có: f(x) =x³+ 2x và f( 3) –f(2) =21

Chọn D.

Đúng(0)

PT

Pham Trong Bach

1 tháng 6 2019

Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là A. 30 B. 24 C. 26 D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

1 tháng 6 2019

Chọn C

Đúng(0)

PT

Pham Trong Bach

22 tháng 9 2019

Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ? A. y =x3-3x+2. B. y=x3+3x+2. C. y=x3-2x+2. D. y...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

22 tháng 9 2019

+ Ta có đạo hàm : f’ (x) = 3ax²+ 2bx+ c.

Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0

Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.

Suy ra: f’(x) = 3x²-3b và f(x) = x³-3x+d.

+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:

f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)

Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2

Khi đó; f( x) =x³-3x+2.

chọn A.

Đúng(0)

PT

Pham Trong Bach

22 tháng 11 2019

Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.Tính giá trị H = f(4) – f(2) A. H = 51 B. H = 54 C. H = 58 D. H =...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

22 tháng 11 2019

Đáp án C

Phương pháp : Xác định hàm số f’(x) từ đó tính được

Cách giải : Ta dễ dàng tìm được phương trình parabol là

Đồ thị hàm số đi qua gốc tọa độ

Đúng(0)

PT

Pham Trong Bach

15 tháng 4 2018

Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A. 7 15 B. 8 15 C. 14 15 D. 16 15 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 4 2018

+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:

Ta có : f’(x) = 4ax³+ 2bx

Đồ thị hàm số y= f’(x) đi qua 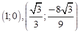ta tìm được a=1 và b= -2

Suy ra hàm số đã cho có dạng: f(x) =x⁴-2x²+d và f’(x) = 4x³-4x.

+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.

Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).

Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1

Vậy hàm số cần tìm là: y =x⁴-2x²+1

+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:

x⁴-2x²+1 =0 nên x=± 1

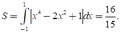
Chọn D.

Đúng(0)

PT

Pham Trong Bach

29 tháng 12 2018

Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương và đồ thị hàm số y= f’ ( x) cho bởi hình vẽ bên. Tìm phần nguyên của giá trị diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A. 2. B. 27. C. 29. D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

29 tháng 12 2018

Ta có đạo hàm : f’ (x) = 3ax²+ 2bx+ c.

Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số y= f’ (x) đi qua 3 điểm

( -1; 0) ; (3; 0) ; (1; -4)

Thay tọa độ 3 điểm này vào hàm f’ ta tìm được: a= 1/3; b= -1; c= -3.

Suy ra: f’ (x) = x²-2x-3 và f(x) = 1/3.x³-x²-3x+d.

Do (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương nên ta có:

F’(x) =0 khi và chỉ khi x=3 ( x= -1 bị loại vì âm)

Như vậy (C) đi qua điểm (3; -9) ta tìm được d=0.

Vậy hàm số đề bài cho là f(x) = 1/3.x³-x²-3x.

Xét phương trình trình hoành độ giao điểm và trục hoành:

. 1 3 x 3 - x 2 - 3 x = 0 ⇔ x = 0 ; x = 3 ± 3 5 2 S = ∫ 3 - 3 5 2 3 + 3 5 2 1 3 x 3 - x 2 - 3 x d x = 29 , 25

Chọn C.

Đúng(0)

DM

Đỗ Mai Huệ

13 tháng 8 2015 - olm

câu 1: cho hàm số y=ax+bXác định giá trị a và b biết đồ thị hàm số đi qua điểm M; m(2;5) và N(1/3;0)câu 2: cho hàm số:y=f(x)=-2x; g(x)=x-1a, tính f(3); g(-2)b, tìm tung độ của điểm A thuộc đồ thị hàm số của điểm A thuộc đồ thị hàm số f(x) có hoành độ là 1/2c.tính hoành độ của điểm B thộc đồ thị hàm số g(x)có tung độ là -3d, điểm C(1/3;-2/3) có thuộc đồ thị hàm số f(x); g(x)...

Đọc tiếp

#Toán lớp 7

2

TH

Trịnh hà hoa

4 tháng 11 2016

Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2

Đúng(0)

HH

Hoàng hậu Bóng Đêm

2 tháng 12 2016

1,04 m

tk mk nha

mk sẽ tk lại

hứa mà

Đúng(0)

LN

lãnh nhật phượng

22 tháng 4 2020 - olm

bài 1 : vẽ đồ thị hàm số của y = f(x) = 4x

a, tìm f(2) ,f(-2),f(4),f(0)

b,giá trị của x khi y = -1,y =0 , y=2,5

bài 2 : cho hàm số y = -3x

a, vẽ đồ thị hàm số trên

b, các diểm M (-2 và 6) có thuộc đồ thị hàm số trên không

c, xác định tọa độ của điểm P nằm trên đồ thị biết tung độ của P là 5

#Toán lớp 7

1

HQ

Huỳnh Quang Sang

22 tháng 4 2020

Bài 1 :

Với x = 1 thì y = 4.1 = 4

Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x

Đường thẳng OA là đồ thị hàm số y = f(x) = 4x

a) Ta có : \(f\left(2\right)=4\cdot2=8\)

\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)

\(f\left(4\right)=4\cdot4=16\)

\(f\left(0\right)=4\cdot0=0\)

b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)

+) y = 0 thì 4x = 0 => x = 0

+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)

Bài 2 :

a) Vẽ tương tự như bài 1

b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :

y =(-3)(-2) = 6

=> Điểm M thuộc đths y = -3x

c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :

=> 5 = -3x => \(x=-\frac{5}{3}\)

Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)

Đúng(0)

OK

OoO Kún Chảnh OoO

21 tháng 12 2015 - olm

cho hàm số y=f(x)=2x

a)tinh f(1);f(1/2);f(-1/2)

b) vẽ đồ thị của hàm số trên

c) biểu diễn hai điểm A(2;-2); B(-1;-2) trên mặt phẳng tọa độ và cho biết điểm nào thuộc , không thuộc đồ thị hàm số :y=2x

d) tìm tọa độ điểm Q , biết điểm Q có tung độ là -6 và thuộc đồ thị hàm số y=2x

#Toán lớp 7

0

OK

OoO Kún Chảnh OoO

21 tháng 12 2015 - olm

cho hàm số y=f(x)=2x

a)tinh f(1);f(1/2);f(-1/2)

b) vẽ đồ thị của hàm số trên

c) biểu diễn hai điểm A(2;-2); B(-1;-2) trên mặt phẳng tọa độ và cho biết điểm nào thuộc , không thuộc đồ thị hàm số :y=2x

d) tìm tọa độ điểm Q , biết điểm Q có tung độ là -6 và thuộc đồ thị hàm số y=2x

#Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP